本記事は、ディープラーニング入門シリーズの第3回目で、こちらの記事を参考にしています。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法) ←イマココ
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
バックプロパゲーション (誤差逆伝播法) とは
バックプロパゲーション (誤差逆伝播法) とは、関数の偏微分を効率的に計算する手法です。
ニューラルネットワークの学習 (損失関数の勾配の計算) を効率よくするために利用します。
例えば、通常の偏微分で20万年かかる計算が、バックプロパゲーションで偏微分すると1週間で済みます。
バックプロパゲーションを説明する方法として、以下の2つの方法があります。
本記事では、直感的に理解しやすい計算グラフを使った方法で説明します。
計算グラフとは
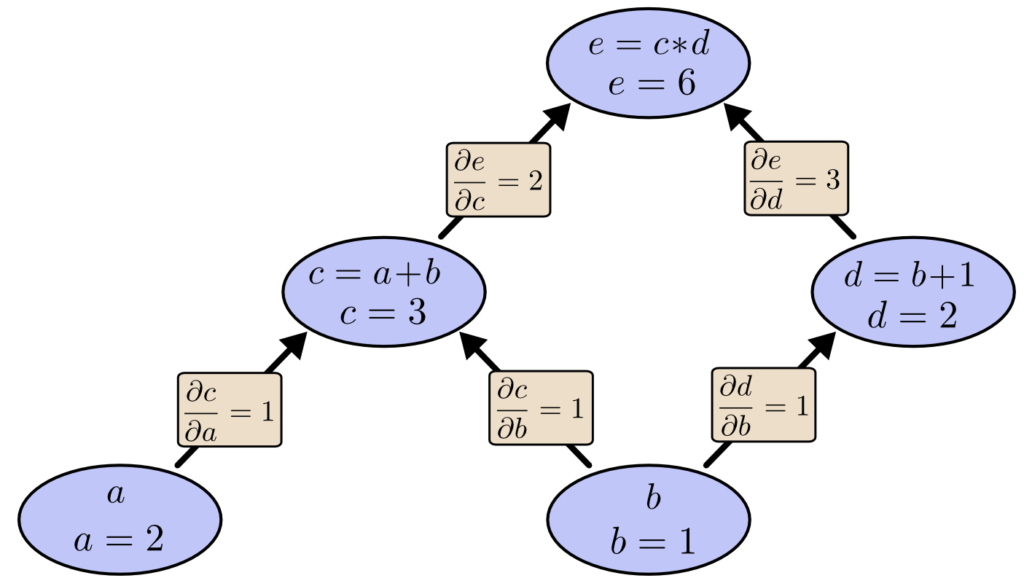
以下の数式を例に計算グラフを説明します。
$$ e = c * d $$
$$ c = a + b $$
$$ d = b + 1$$
上記の数式を、計算グラフで表すと以下のとおりです。
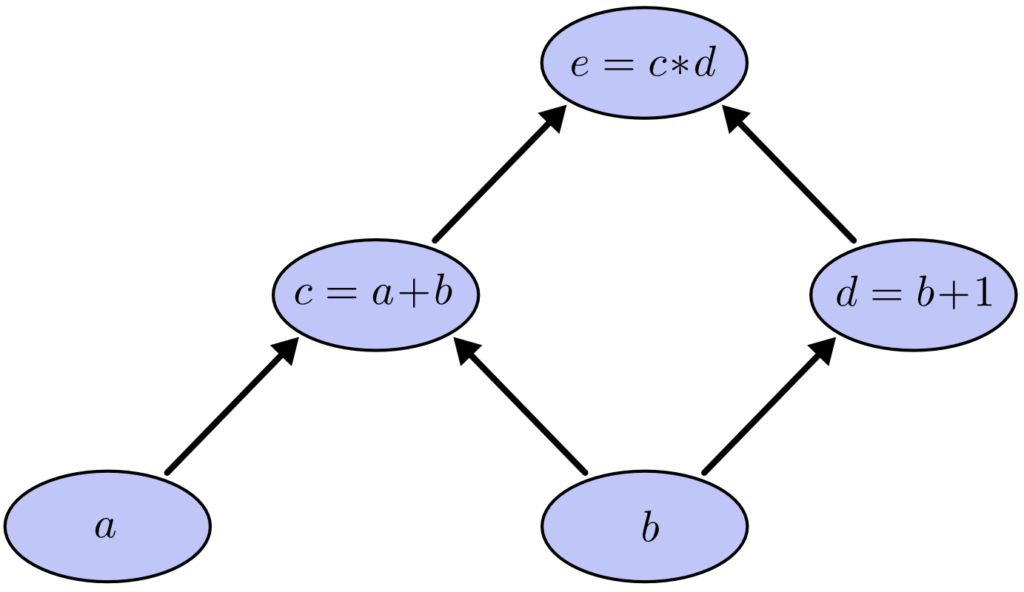
この時、a =2, b= 1 とすると、計算グラフを利用して e = 6 と計算できます。
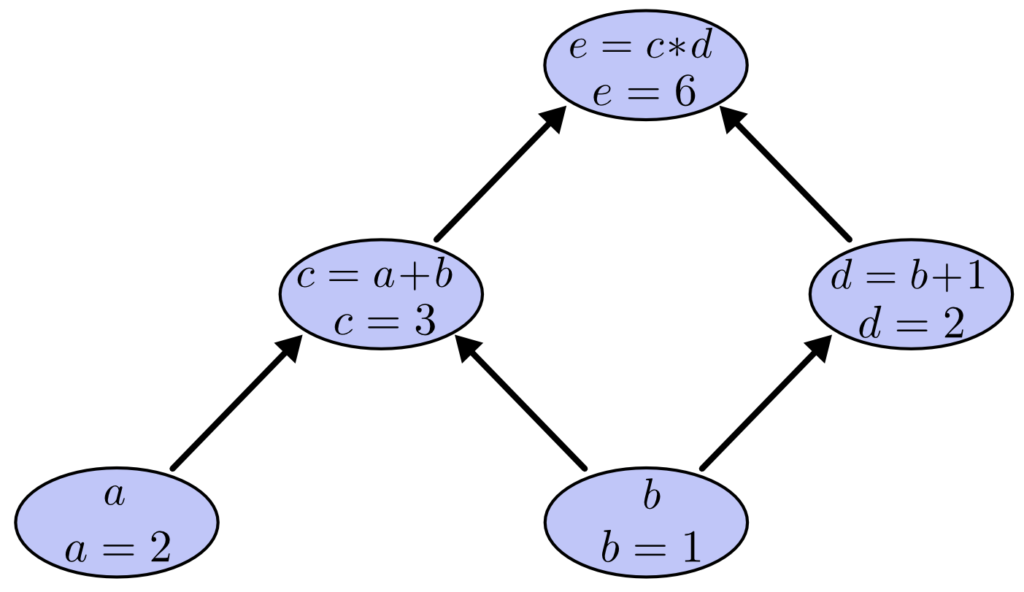
計算グラフを用いた偏微分
バックプロパゲーションの目標は、損失関数を重み W で偏微分して勾配を求めることです。
そのため、ここでは計算グラフを用いた関数の偏微分を説明します。
直接繋がるノードの偏微分
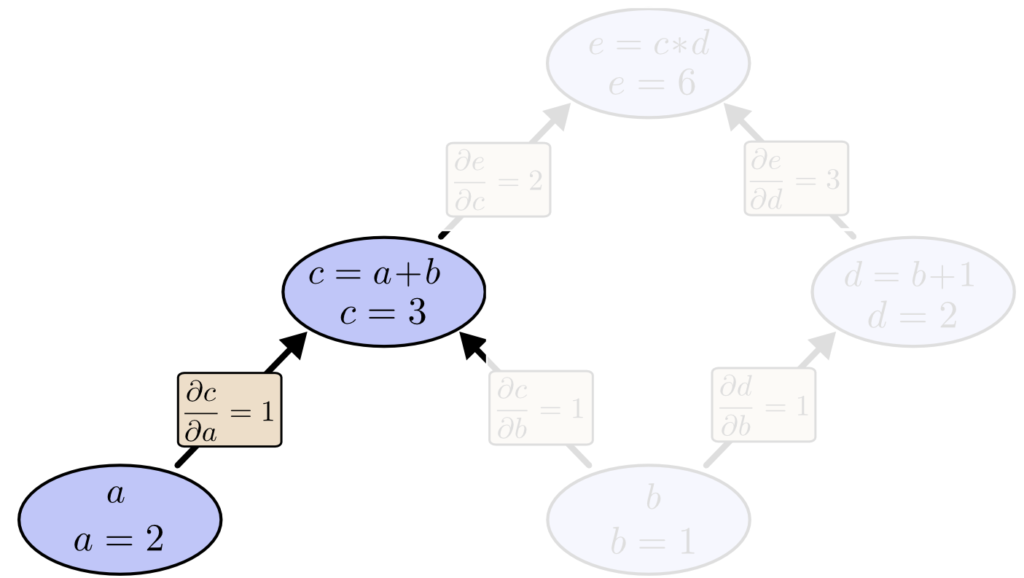
関数 c を a で偏微分します。(∂c/∂a を求めます)
$$ \frac{∂c}{∂a} = \frac{∂(a+b)}{∂a} =\frac{∂a}{∂a} + \frac{∂b}{∂a} = 1 + 0 = 1 $$
つまり、a が 0.1 増えると、c は 0.1 増えます。(a = 2.1 になると、c = 3.1 になります。)
直接繋がらないノードの偏微分
直接繋がらないノードの偏微分 (例:関数 e を a で偏微分) には、連鎖律を利用します。
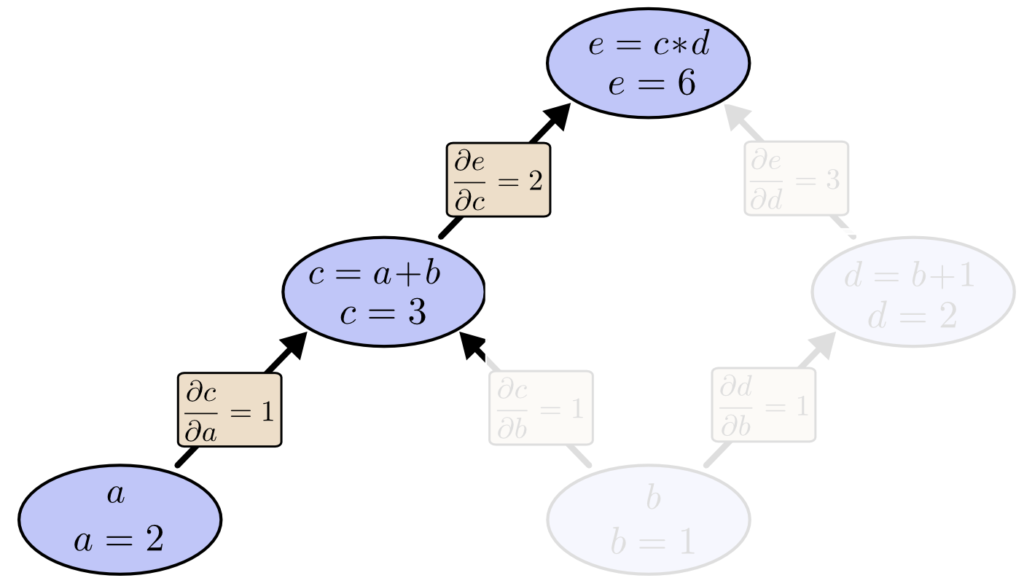
数式で表すと以下のとおりです。(N はゴールまでの経路の数、y_i は経路上のノード)
$$ \frac{∂z}{∂x} = \sum_{i=1}^N \frac{∂z}{∂y_i} * \frac{∂y_i}{∂x} $$
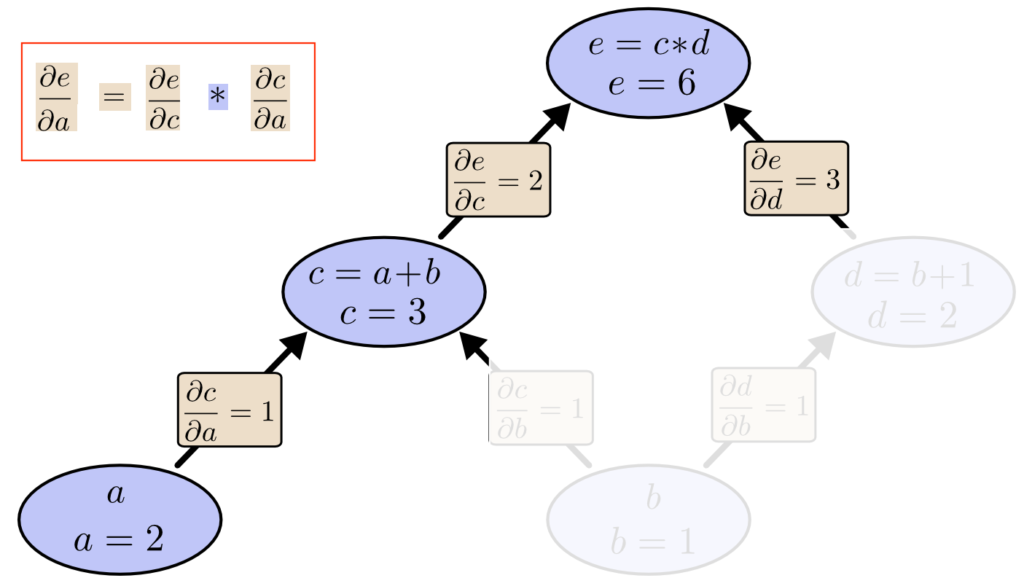
連鎖律を利用して、関数 e を a で偏微分 (単数経路)
連鎖律を利用して、関数 e を a で偏微分した結果 (微分係数 ∂e/∂a) を次のように求めます。
$$ \frac{∂e}{∂a} = \frac{∂e}{∂c} * \frac{∂c}{∂a} = 2 * 1 = 2 $$
つまり、a が 0.1 増えると、e は 0.2 増えます。(a = 2.1 になると、c = 3.1, e = 6.2 になります。)
※補足 ∂e/∂c の求め方
$$ \frac{∂e}{∂c} = \frac{∂cd}{∂c} = d = 2 $$
連鎖律を利用して、関数 e を b で偏微分 (複数経路)
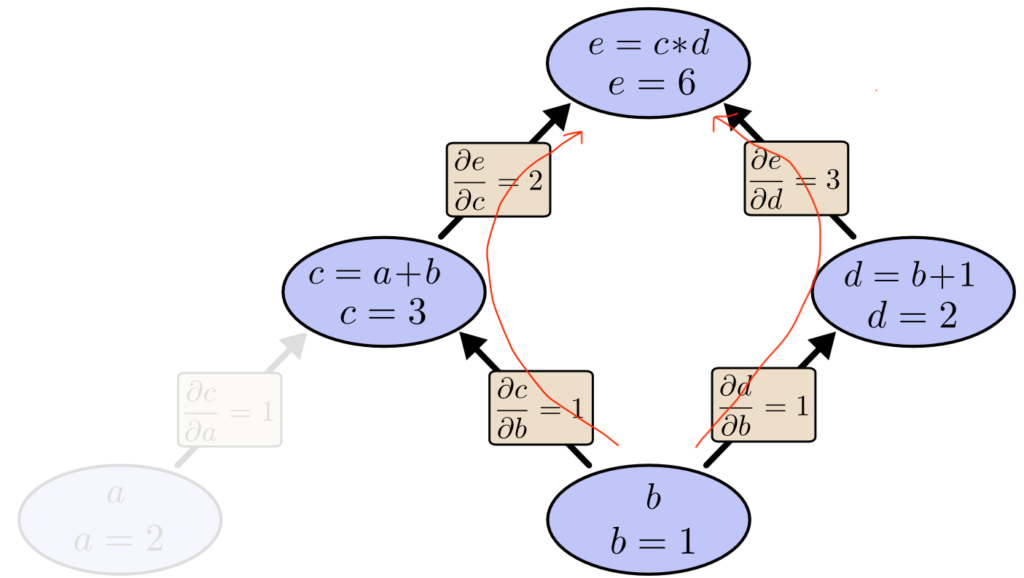
連鎖律を利用して、関数 e を b で偏微分した結果 (微分係数 ∂e/∂b) を次のように求めます。
$$ \frac{∂e}{∂b} = \left(
\frac{∂e}{∂c} * \frac{∂c}{∂b}
\right) +
\left(
\frac{∂e}{∂d} * \frac{∂d}{∂b}
\right)
= 2 * 1 + 3 * 1= 5 $$
つまり、b が 0.1増えると、e は 0.5 増えます。
(b = 1.1 になると、c = 3.1, d= 2.1 e = 6.51 ※になります。)
※∂ は 0.1 より微小な数字です。例でe が 0.5 ではなく、0.51 増加していますが、0.1 を ∂ に近づけると 0.5 になります。
因数分解による計算量の削減
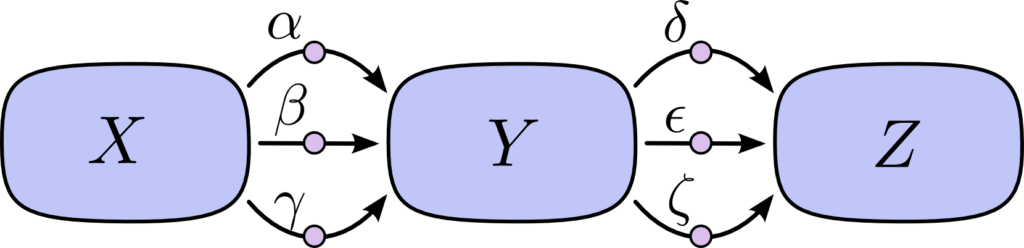
上の図において、連鎖律を用いて Z を X で偏微分する場合、以下のように表せます。
$$ \frac{∂Z}{∂X} = αδ + αε + αζ + βδ + βε + βζ + γδ + γε + γζ $$
今の時点で 3 * 3 = 9 通りの経路がありますが、さらに経路の組み合わせが増えると、計算量が爆発します。
そこで、上記の式を因数分解することで計算量を減らします。
$$ \frac{∂Z}{∂X} = (α+β+γ)(δ+ε+ζ) $$
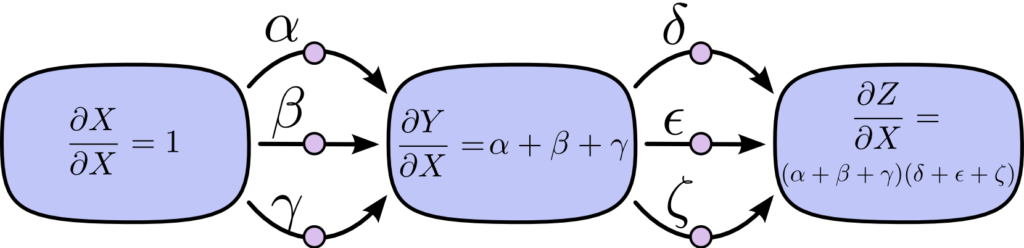
伝播の種類とメリット・デメリット
連鎖律を利用した微分では、伝播する向き (計算する順番) が2種類存在します。
- 順伝播 (フォワードモード微分)
- 逆伝播 (リバースモード微分) = バックプロパゲーション (誤差逆伝播法)
順伝播 (フォワードモード微分) を利用して、∂Z/∂X を求める方法は以下のとおりです。
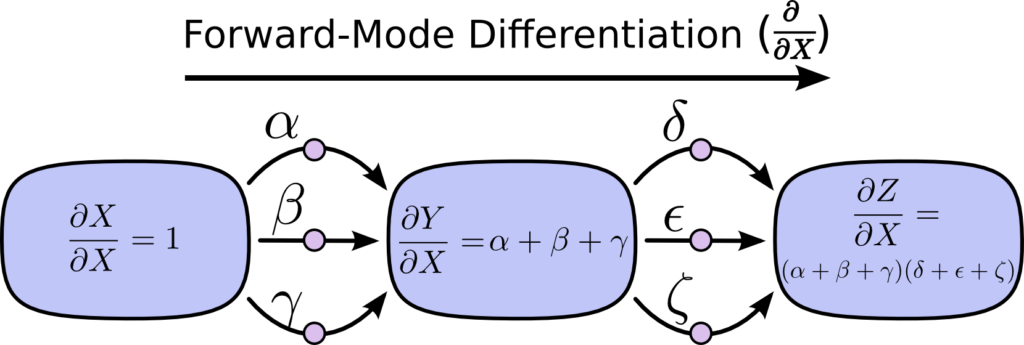
逆伝播 (リバースモード微分)を利用して、∂Z/∂X を求める方法は以下のとおりです。

順伝播 vs 逆伝播
伝播を逆にするとどんなメリットがあるのでしょうか。
結論から言うと、逆伝播は「入力層の数 > 出力層」の時、数計算量が少なくなります。
以下を例に、順伝播 (フォワードモード微分)と逆伝播 (リバースモード微分) の計算量を比較します。
順伝播 (フォワードモード微分) の場合
入力層 b から順伝播 (フォワードモード微分) すると、以下のように b に対するすべての微分係数を取得できます。
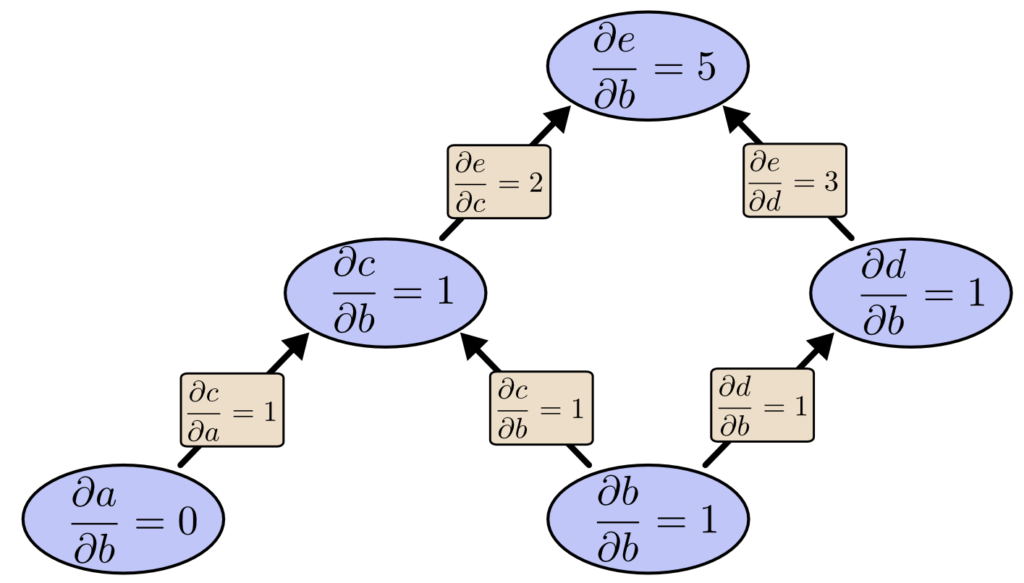
入力層 a に対する微分係数は、別途 a から 順伝播 (フォワードモード微分) が必要です。
逆伝播 (リバースモード微分) の場合
出力層 e から逆伝播 (リバースモード微分) すると、以下のようにすべての微分係数を取得できます。
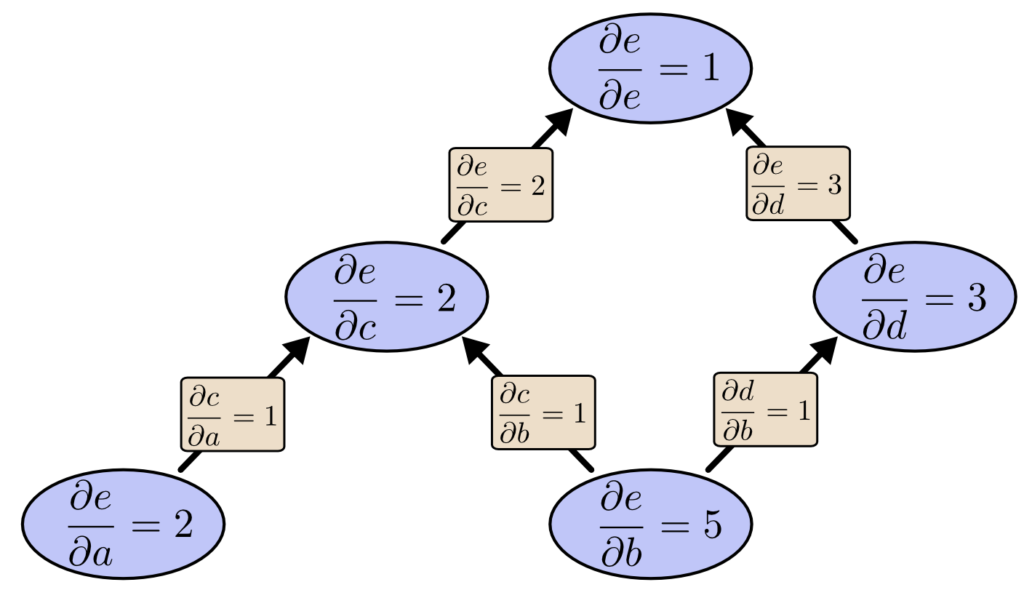
1回の逆伝播 (リバースモード微分) で、入力層 a, b 両方の微分係数を求めることができました。
つまり、先程の順伝播と比較して2倍の計算速度であることがわかります。
今回は「入力層が2つ、出力層が1つ」の例を示しましたが、「入力層が1万」の場合は、逆伝播 (リバースモード微分) のほうが1万倍早くなります。
※逆に「入力層が1つ、出力層が1万」の場合は順伝播 (フォワードモード微分) のほうが1万倍早いです。
勾配降下法と逆伝播
逆伝播 (リバースモード微分)、つまりバックプロパゲーションにより、確率的勾配法 SGD アルゴリズムの手順2 [勾配の算出] で行う、偏微分の計算が早くなります。
1. 学習用の大量のデータ (訓練データ) から一部のデータを選ぶ [ミニバッチ学習]
https://hogetech.info/machine-learning/deep-learning/intro2/#sgd
2. 重み W が適切かどうか判断する指標が、良くなる方向を算出 [損失関数の勾配を算出]
3. 重み W を指標がよくなる方向に、学習率 (任意の定数) の分だけ更新 [勾配降下法]
4. 1に戻る
関連記事
ディープラーニング入門記事の続きは以下のとおりです。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法) ←イマココ
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
参考資料