本記事は、ディープラーニング入門シリーズの第2回目です。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク ←イマココ
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
パーセプトロン (人工ニューロン) とは
まずは、単純な人間の脳の仕組みを示します。
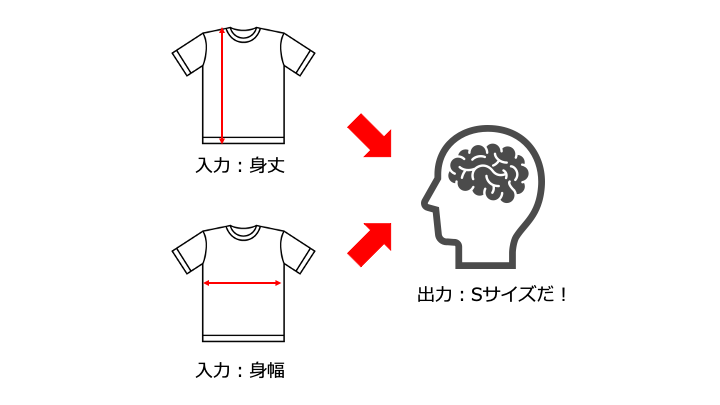
この脳の仕組みをパーセプトロンで表現すると、以下のとおりです。
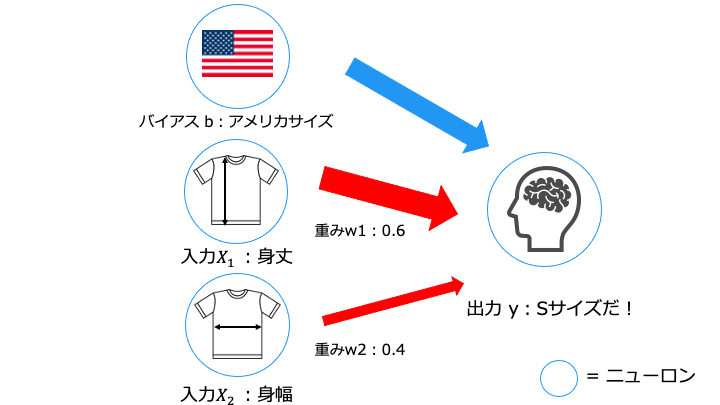
| パーセプトロンの構成要素 | 説明 |
|---|---|
| 入力 X | 入力する値 パーセプトロンが答えを出すための判断材料 |
| 重み W | 各入力をどれだけ重視するか |
| バイアス b | しきい値 出力 Y がどれだけ活性化しやすいか (0-->1 に切り替わりやすさ) (後述の活性化関数を参照) |
| 出力 Y | 出力する値 入力に対する答え |
数式と活性化関数
パーセプトロンを数式で表すと以下のとおりです。
$${y = \left\{\begin{array}{ll}
0 & (b+w_1x_1+w_2x_2 \leq 0) \\
1 & (b+w_1x_1+w_2x_2 \gt 0) \\
\end{array} \right. }$$
なお、重み付き入力とバイアスの総和を元に、出力を決定する関数を活性化関数と言います
(パーセプトロンの活性化関数は、「総和 ≦ 0 なら0」、「総和 > 0 なら1」を出力)
パーセプトロンの例
「身丈によってシャツのサイズ」から「Sサイズ」か「Mサイズ」を判断するパーセプトロンは、以下の数式で表現します。※1
$${y = \left\{\begin{array}{ll}
Sサイズ & (-69cm + 身丈 \times 1 \leq 0) \\
Mサイズ & (-69cm + 身丈 \times 1 \gt 0) \\
\end{array} \right. }$$
※1
https://www.uniqlo.com/jp/ja/products/E422992-000/00?colorDisplayCode=02&sizeDisplayCode=004
・重み w1(身丈) = 1, w2(身幅) = 0 (つまり身丈だけで判断)
・バイアス b = -69cm の場合 (ユニクロの「身丈 M サイズ = 69」より)
単純パーセプトロンとは
先程紹介したパーセプトロンは単純パーセプトロンと呼ばれます。
$$ {y = \left\{\begin{array}{ll}
0 & (b+w_1x_1+w_2x_2 \leq 0) \\
1 & (b+w_1x_1+w_2x_2 \gt 0) \\
\end{array} \right. } $$
この単純パーセプトロンの活性化関数をグラフに表すと以下のとおりです。
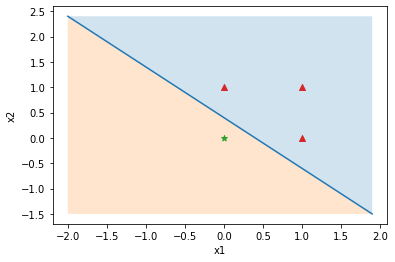
x2 = -x1 - 0.4 (つまり直線を表す y = ax+ b の形になる)
つまり単純パーセプトロンとは、線形関数 (1本の直線) で活性化関数で、2つのグループに分割する方法です。
単純パーセプトロンの限界
単純パーセプトロンでは、分割できないパターン (線形分離不可能) が存在します。
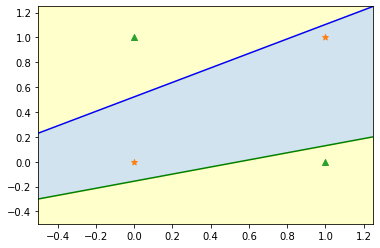
例えば、以下の領域では、線形関数 (1本の直線) で「☆グループ」と「△グループ」に分割できません。

実際に試してみますが、やはり無理なことがわかります。
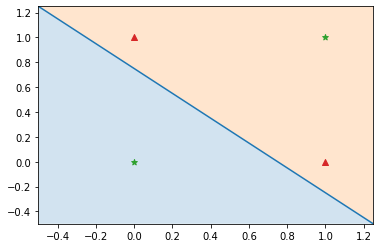
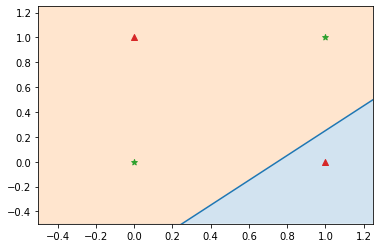
このような領域を分割するために、以下の2つの方法を利用します。
多層パーセプトロンとは
多層パーセプトロンとは、以下の2つの特徴を持つパーセプトロンです。
多層パーセプトロン(たそうパーセプトロン、英: Multilayer perceptron、略称: MLP)
https://ja.wikipedia.org/wiki/%E5%A4%9A%E5%B1%A4%E3%83%91%E3%83%BC%E3%82%BB%E3%83%97%E3%83%88%E3%83%AD%E3%83%B3
MLPは少なくとも3つのノードの層からなる。入力ノードを除けば、個々のノードは非線形活性化関数を使用するニューロンである
パーセプトロンの層を追加
パーセプトロンの層を追加するとは、以下のように中間層 (隠れ層) を追加することです。
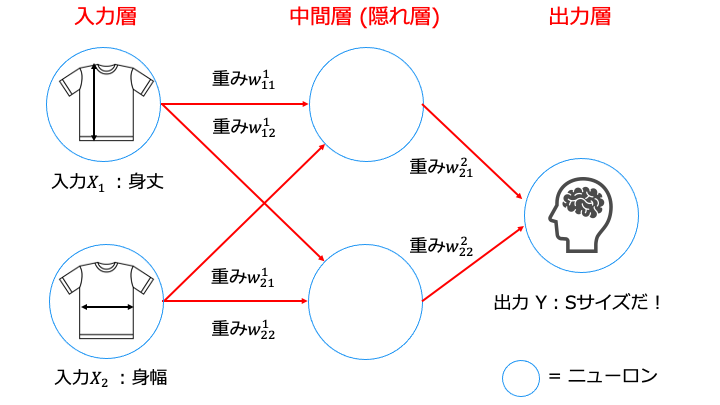
層を追加することにより、前の層のグループ分けの結果を次の層で利用できます。
(つまり、層ごとに異なる特徴でグループ分けすることができます。)
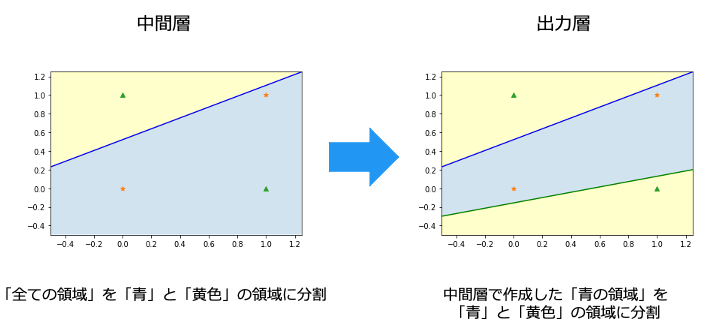
層を追加することで、「☆グループ」と「△グループ」で領域を分けられるようになりました。
活性化関数に非線形関数を利用
層を追加する際に、出力層の活性化関数が線形関数 (1本の直線) の場合は、意味がありません。
そこで、層を追加する場合は、活性化関数に非線形関数 (曲線/複数の線) を利用します。

結論
ここで多層パーセプトロンの定義に戻ります。
多層パーセプトロンとは、以下の2つの特徴を持つパーセプトロンです。
・少なくとも3つの層がある (入力層、中間層 (隠れ層) 1層、出力層)
#mlp
・活性化関数に非線形関数を利用
これは、上記2つの特徴を満たすと、全てのパターンで領域を分割可能なことが証明されているからです。(= 普遍性定理)
なお、理論上、中間層 (隠れ層) は1層でよいと言われてます。
しかし、入力 X の数が増えると、重み W の値の設定が複雑になるため、一般的には中間層を複数用意して、段階的に領域を分割します。
(参考資料 https://ml4a.github.io/ml4a/jp/looking_inside_neural_nets/)
ニューラルネットワークとは
多層パーセプトロンは人工ニューラルネットワークの1種です。
多層パーセプトロンは時折、特に単一の隠れ層を持つ時、「バニラ」ニューラルネットワークと口語的に呼ばれることがある
https://ja.wikipedia.org/wiki/%E5%A4%9A%E5%B1%A4%E3%83%91%E3%83%BC%E3%82%BB%E3%83%97%E3%83%88%E3%83%AD%E3%83%B3
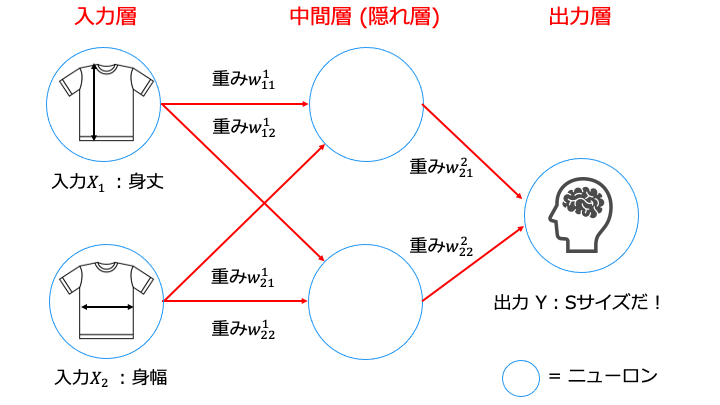
なぜなら、パーセプトロン = 「人工ニューロン (脳の神経細胞) 」を多層に「繋げた」ものだからです。
機械学習とニューラルネットワークの違い
ニューラルネットワークはデータの特徴量 (「数字の判定は形」、「T シャツのサイズは身丈」など) を機械が見つけます。
| 従来の機械学習 | ニューラルネットワーク | |
|---|---|---|
| 特徴量 | 人が特徴を見つける (SIFT, SURF, HOG) | 機械が特徴を見つける (ニューラルネットワーク) |
| 識別器 | 機械が特徴から規則性を見つける (SVM, KNN) | 機械が特徴から規則性を見つける |
つまり、大量のデータさえ用意すれば、人が介入することなくパターンを学習できます。(数字であろうと、T シャツのサイズであろうと関係なく学習可能)
推論可能な問題の種類
ニューラルネットワークは以下の2つの問題を推論できます。
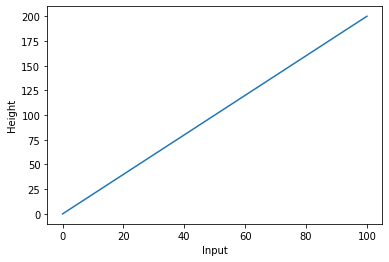
例えば、写真に映る人 (データ) を、身長「何センチ」か推測する問題です。
ニューラルネットワークの出力層が出力する値は Y = f(X) の Y となります。(入力は X)
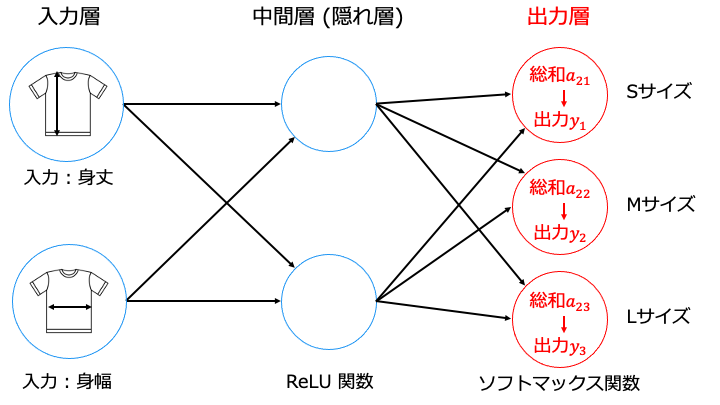
例えば、写真に映る人 (データ) を、服のサイズ「S」・「M」・「L」の3クラスに分類する問題です。
出力層のニューロンの数はクラス (グループ) の数、出力値は各クラスに該当する確率等になります。
ニューラルネットワークの流れ
ニューラルネットワークは主に2つのフェーズに分かれます。
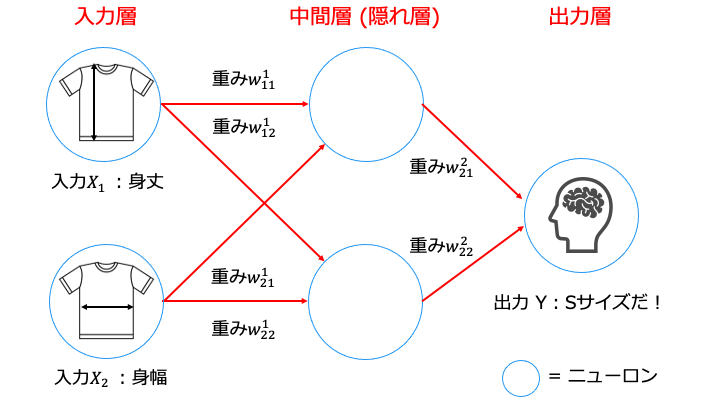
ニューラルネットワークの推論
ニューラルネットワークでは、以下の手順で推論を行います (入力 X から出力 Y を求めます) 。
※各用語は後述します。
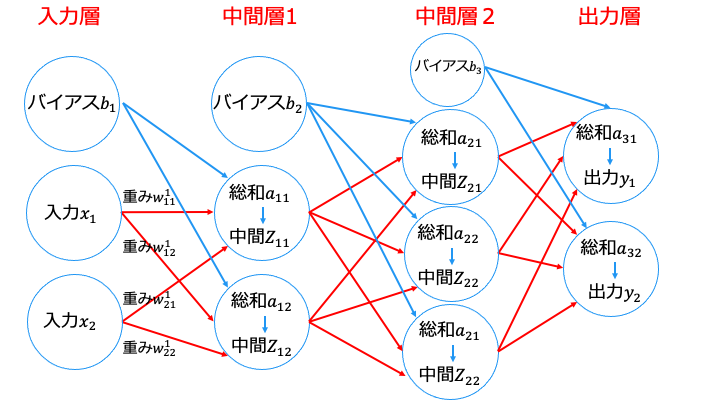
- 各総和 a (全結合層 A) を求めます※
- 各総和 a (全結合層 A) に対して活性化関数を適用します
- 中間層 (隠れ層) の場合は、中間 Z を次の入力として手順1に戻ります。
出力層の場合は終了します
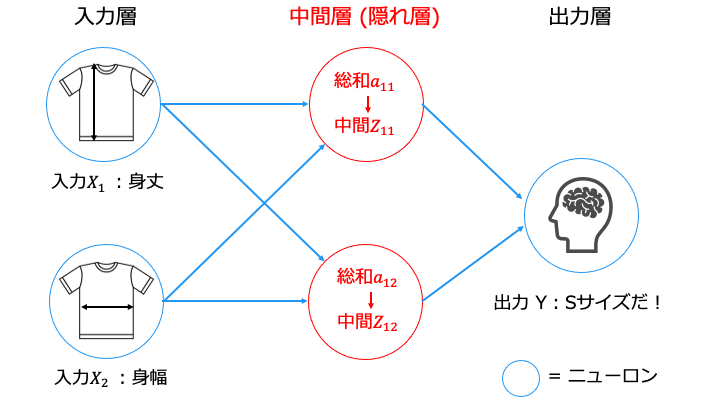
※「中間層」と「出力層」は、以下のように「全結合層」と「活性化関数」から構成されます。
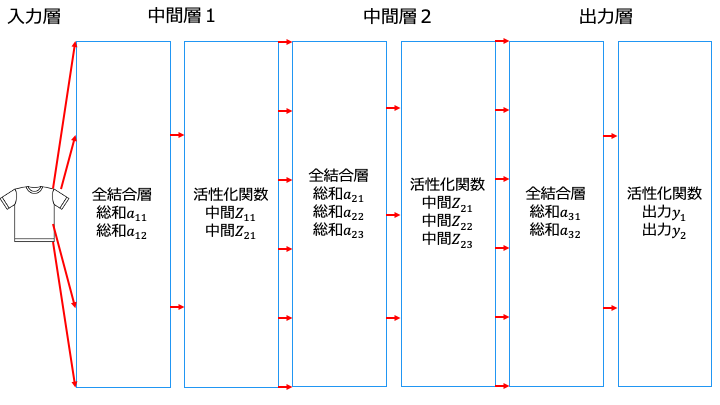
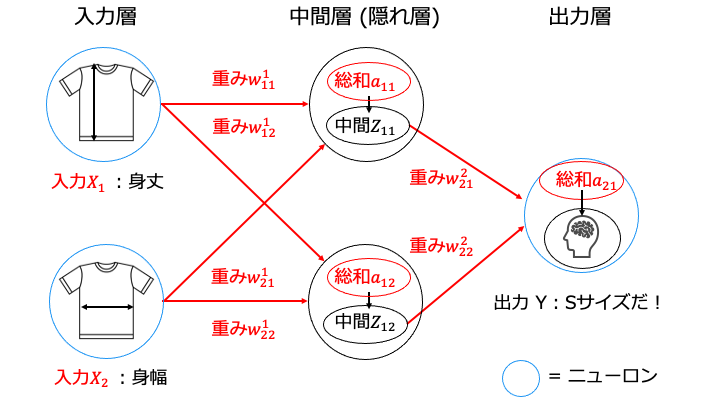
と考えると良い
全結合層の数式は以下のとおりです。(パーセプトロンの数式から活性化関数を除いたもの)
$${A_1 = \left\{\begin{array}{ll}
a_{11} = (b_1+w ^{1}_{11}x_1+w ^{1}_{12}x_1) \\
a_{12} = (b_1+w ^{1}_{21}x_2+w ^{1}_{22}x_2) \\
\end{array} \right. }$$
これは以下のように行列で表現でき、Python で簡単に計算できます。
$$ A = \begin{pmatrix}
a_1 & a_2
\end{pmatrix},
B = \begin{pmatrix}
b_1 & b_2
\end{pmatrix},
X = \begin{pmatrix}
x_1 & x_2
\end{pmatrix},
W = \begin{pmatrix}
w ^{1}_{11} & w ^{1}_{21} \\
w ^{1}_{12} & w ^{1}_{22} \\
\end{pmatrix} $$
$$ A_1 = B + X * W $$
Python での実装例
import numpy as np B = np.array([0,1]) X = np.array([2,3]) W = np.array([[4,5],[6,7]]) A1 = B + np.dot(X, W) print(A1)
中間層 (隠れ層) の活性化関数
中間層では、全結合層に次のいずれかの活性化関数 (非線形関数) を利用します。
基本的に ReLU 関数を使っておけば良さそうです。(参考資料1、2)
シグモイド関数の数式は以下のとおりです。
$$ h(x) = \frac{1}{1 + exp(-x)} $$
シグモイド関数をグラフで表現すると以下のとおりです。
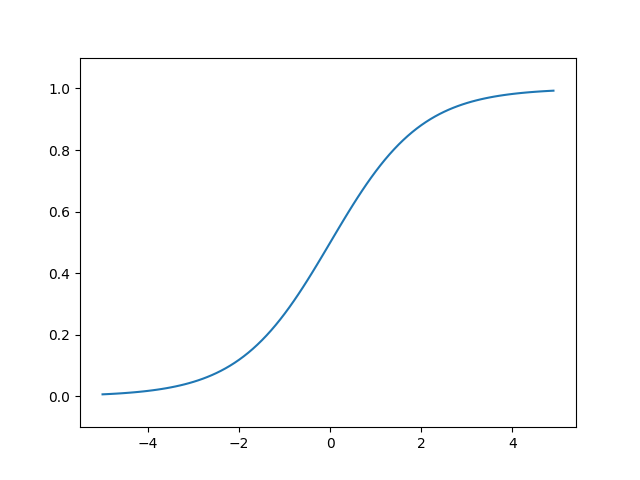
import numpy as np import matplotlib.pylab as plt def sigmoid(x): return 1 / (1 + np.exp(-x)) X = np.arange(-5.0, 5.0, 0.1) Y = sigmoid(X) plt.plot(X, Y) plt.ylim(-0.1, 1.1) plt.show()
$$ {h(x) = \left\{\begin{array}{ll}
x & (x \gt) \\
0 & (0 \leq) \\
\end{array} \right. } $$
ReLU 関数 (ランプ関数) をグラフで表現すると以下のとおりです。
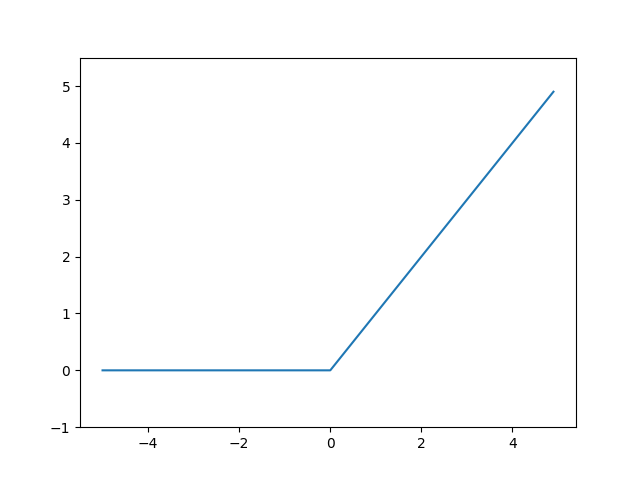
# coding: utf-8
import numpy as np
import matplotlib.pylab as plt
def relu(x):
return np.maximum(0, x)
x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()
出力層の活性化関数の使い方
出力層では、全結合層に適用する活性化関数を、推論したい問題によって次のように選択します。
恒等関数を表現する式は以下のとおりです。(つまり何もしなくていいです。)
$$ a = f(a) $$
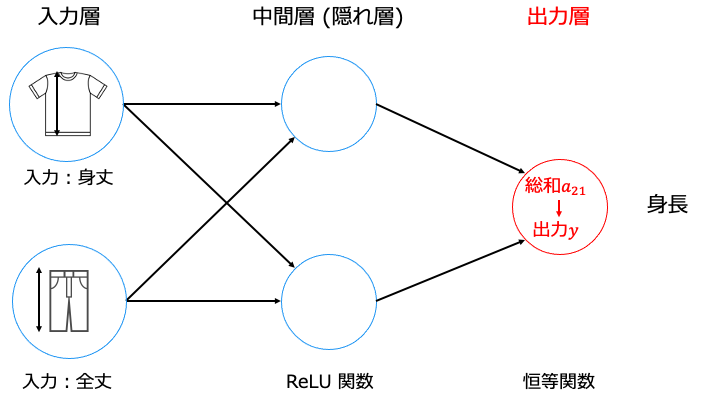
ニューラルネットワークが予測した身長は a12 の値となります。
ソフトマックス関数を表現する式は以下のとおりです。
$$ y_k = \frac{exp(a_k)}{\sum_{i=1}^{n} exp(a_i)} $$
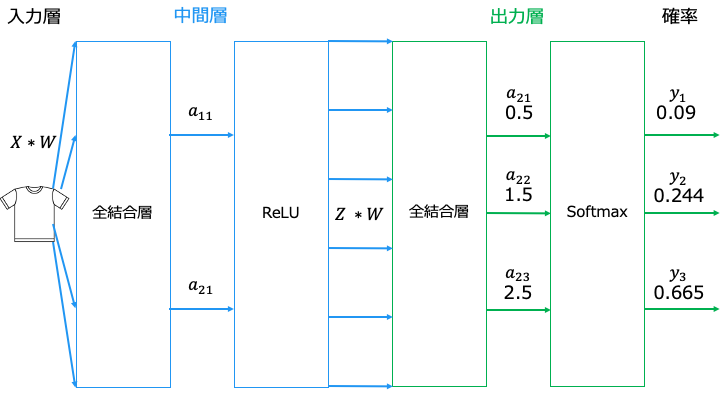
例えば、出力層の A2 (a21, a22, a23) = [0.5, 1.5, 2.5] に、ソフトマックス関数を利用してみます。
import numpy as np
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c) #オーバーフロー対策
sum_exp_a = np.sum(exp_a)
y = exp_a / sum_exp_a
return y
a = np.array([0.5, 1.5, 2.5])
y = softmax(a)
print(y)
[0.09003057 0.24472847 0.66524096]
それぞれ「S サイズは 9.0%」・「M サイズは 24.4%」・「L サイズは 66.5%」
よってこのニューラルネットワークは、入力したシャツのサイズは、確率の一番高い L サイズだと判定します。
ソフトマックス関数の前後で値の大小関係は変わりません。
・ソフトマックス関数前:[0.5 < 1.5 < 2.5]
・ソフトマックス関数後:[0.09003057 < 0.24472847 < 0.66524096]つまり、単に分類問題を分類する場合、ソフトマックス関数は必要ありません。(一番値の大きいものを選べばいい)
ソフトマックス関数は、「分類問題の出力を確率で取得したい場合」や「ニューラルネットワークの学習」に利用します。
推論のまとめ
これまでの内容をまとめると、ニューラルネットワークで推論は以下の手順となります。
ニューラルネットワークの学習
例えば、以下の 28 * 28 ピクセルの画像では、入力 X は 784 個となります。
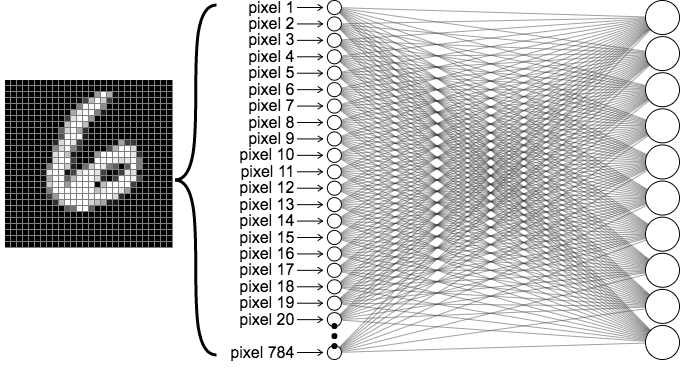
この 784 個の入力 X に対して、以下のようにニューロンの数だけ重み W を設定する必要があります。

しかし、この膨大な数の重み W (とバイアス B) の値を、手作業で設定するのは現実的ではありません。
そこで、ニューラルネットワークの学習 (大量の学習用の画像データ[= 訓練データ] を見せること) により、自動で適切な重み W を設定します。
以降では、ニューラルネットワークの学習で利用する最適化アルゴリズムの1つである「確率的勾配法 (SGD) 」を用いて、自動で適切な重み W を設定する方法を説明します。
その他の最適化アルゴリズムについては、以下の記事をご覧ください。
※各用語については後述します。
- 学習用の大量のデータ (訓練データ) から一部のデータを選ぶ [ミニバッチ学習]
- 重み W が適切かどうか判断する指標が、良くなる方向を算出 [損失関数の勾配を算出]
- 重み W を指標がよくなる方向に、学習率 (任意の定数) の分だけ更新 [勾配降下法]
- 1に戻る
つまり、標本調査です。
統計調査によって何かを調べたい時、例えばある中学校で全校生徒の平均身長を調べたいと思ったら、生徒全員の身長を測って平均を計算すれば正確な結果が得られます。このように、対象となるすべてを調べる調査を「全数調査」といいます。一つの中学校の全生徒の身長を調べることは、それほど大変な手間ではないでしょうが、日本中のすべての中学生の身長を調べるのは大変な手間と費用がかかります。このような場合には、手間や費用を省くために、一部の人だけを選んで調べる方法もあります。このような調査を「標本調査」といいます。
https://www.stat.go.jp/teacher/survey.html
ミニバッチ学習 (全部の訓練データを使わず、一部のデータのみ) を使う理由としては、後述する損失関数の計算量が多すぎるからです。
ニューラルネットワークの学習 (適切な重み W の自動設定) とは、損失関数を0に近づける(=予測の正解数を増やす) W の値を探すことです。
よく利用する損失関数は以下の2つです。
2乗和誤差を数式で表すと以下のとおりです。(y は予測、t は正解)
$$ E = \frac{1}{2}\sum_{k} (y_k-t_k)^2 $$
なお、以下の計算は2乗和誤差をより使いやすくするためのものであり、数式の意味に影響は与えません。
- 合計を2乗するのは、正の数にしたいからです。
- 合計を 1/2 するのは、後述する微分で指数2と打ち消し合う計算の都合です。
2乗和誤差の実装例は以下のとおりです。(0 ~ 9 まで 10 種類の文字を分類するニューラルネットワーク)
import numpy as np
def mean_squared_error(y, t):
return 0.5 * np.sum((y-t)**2)
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] # 数字の「2」が正解
#正しい予測:数字の「2」である確率は 0.6 = 60%の場合
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
result = mean_squared_error(np.array(y), np.array(t))
print("正しい予測の場合:%f" % result)
#誤った予測:数字の「6」である確率が80%の場合
wrong_y = [0.1, 0.05, 0.0, 0.0, 0.05, 0.0, 0.8, 0.0, 0.0, 0.0]
result = mean_squared_error(np.array(wrong_y), np.array(t))
print("誤った予測の場合:%f" % result)
正しい予測の場合:0.097500 誤った予測の場合:0.827500
正しい予測のほうが、損失関数が小さいことがわかります。
交差エントロピー誤差を数式で表すと以下のとおりです。(y は予測、t は正解なら1、不正解なら0)
$$ E = -\sum_{k} t_k \log y_k $$
交差エントロピー誤差の実装例は以下のとおりです。
(0 ~ 9 まで 10 種類の文字を分類するニューラルネットワーク)
import numpy as np
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta))
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] # 数字の「2」が正解
#正しい予測:数字の「2」である確率は 0.6 = 60%の場合
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
result = cross_entropy_error(np.array(y), np.array(t))
print("正しい予測の場合:%f" % result)
#誤った予測:数字の「6」である確率が80%の場合
wrong_y = [0.1, 0.05, 0.0, 0.0, 0.05, 0.0, 0.8, 0.0, 0.0, 0.0]
result = cross_entropy_error(np.array(wrong_y), np.array(t))
print("誤った予測の場合:%f" % result)
正しい予測の場合:0.510825 誤った予測の場合:16.118096
正しい予測のほうが、損失関数が小さいことがわかります。
損失関数を利用する理由
損失関数ではなく、予測正解率じゃ駄目なのか?と疑問に思った方がいるかもしれません。
損失関数を利用する利点は、予測の大小を表現できることです。
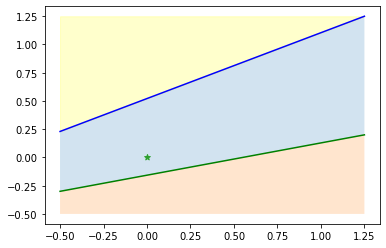
例えば、以下の分類問題で「予測 = ☆の座標(の領域)」「正解は黄色の領域」だったとします。
この時、次の2つ次のどちらの予測が良い予測といえるでしょうか。
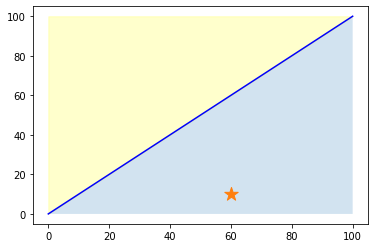
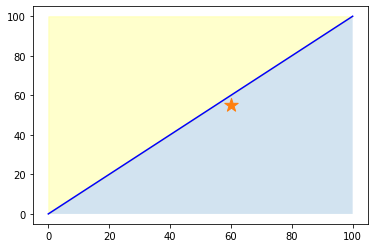
どちらも予測自体は間違いですが、右の予測の方が正解の黄色領域に近いため良い予測と言えます。
そのため、予測正解率ではなく、損失関数を利用します。
では、ここからは損失関数を減らす方法として、勾配降下法を紹介します。
例えば、重み W (w0, w1) からなる、以下の関数を考えます。
$$ f(w_0 , w_1) = {w_{0}}^{2} + {w_{1}}^{2} $$
上記の関数に対する勾配 grad f と、勾配のマイナス方向 -grad f は以下のとおりです。
$$ grad f = (2w_0, 2w_1)$$
$$-grad f = (-2w_0, -2w_1)$$
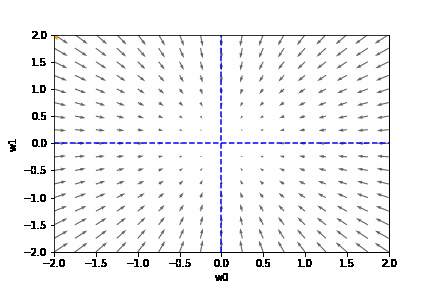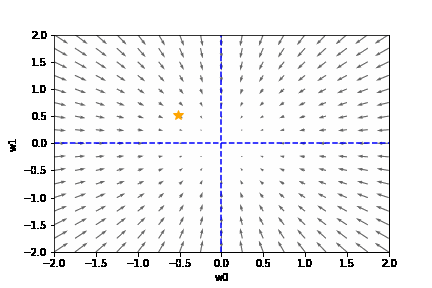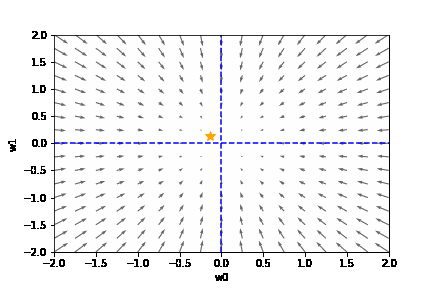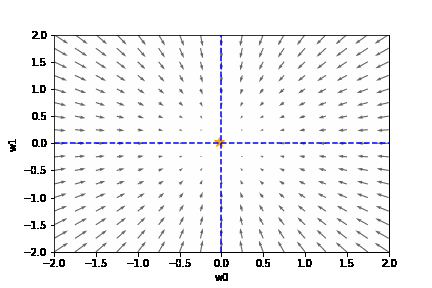
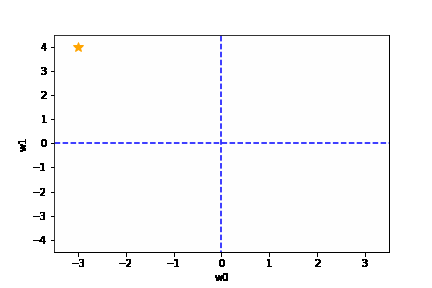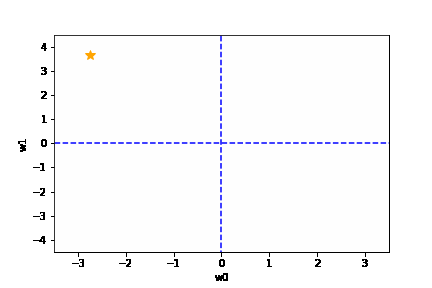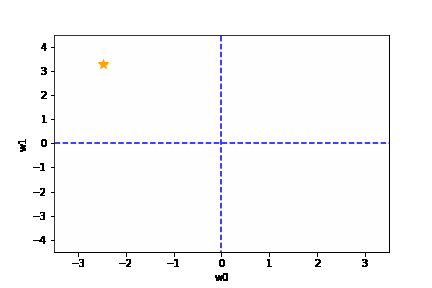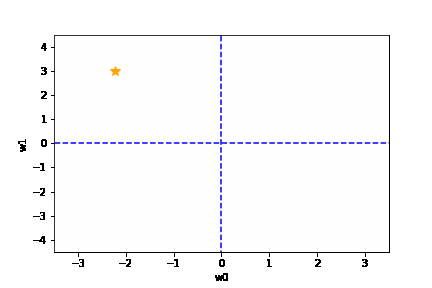
上記の関数 f(w_0 , w_1) と、-grad f をグラフで表すと以下のとおりです。
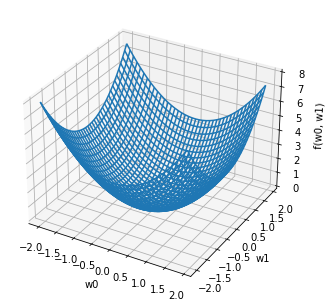
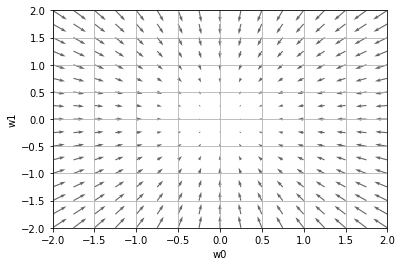
ソースコード https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/gradient_2d.py
上のグラフから次の2つのことが読み取れます。
- 関数 f(w0, w1) は、(w0, w1) = (0, 0) の時、最も小さくなる
- マイナス方向の勾配 -grad f は、(w0, w1) = (0, 0) の方向を示す
つまり、勾配のマイナス方向に進むことで損失関数を減らせることがわかります。
以下のように重み W を、勾配 (∂L/∂W) のマイナス方向に移動すると、損失関数が減少することがわかります。
$$ W ← W - \frac{∂L}{∂W} $$
数式で表すと以下のとおりです。(W は重み、← は代入、ηは学習率、∂L/∂W は勾配)
$$ W ← W - \eta \frac{∂L}{∂W} $$
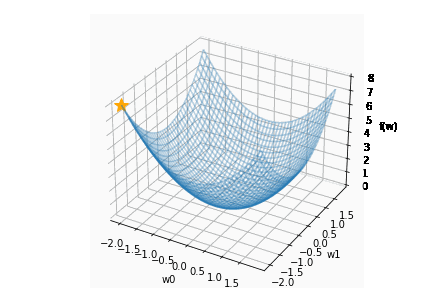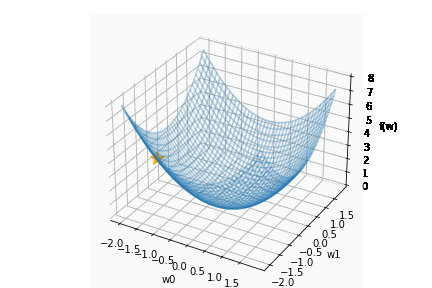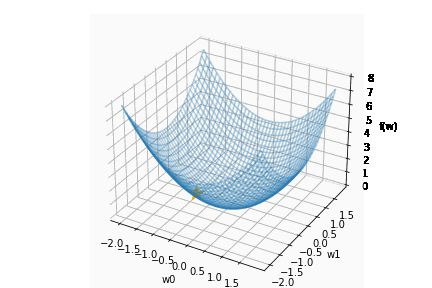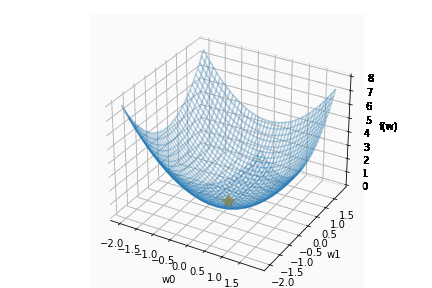
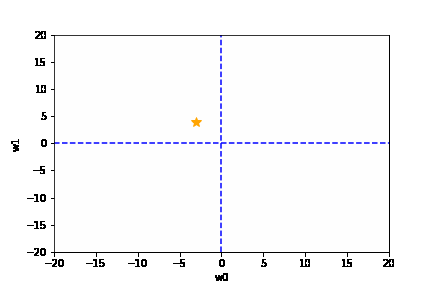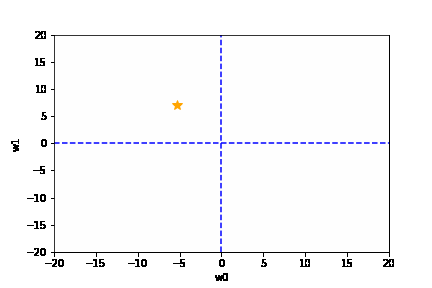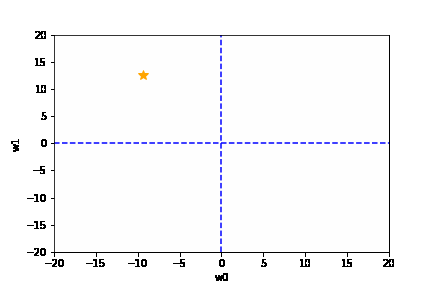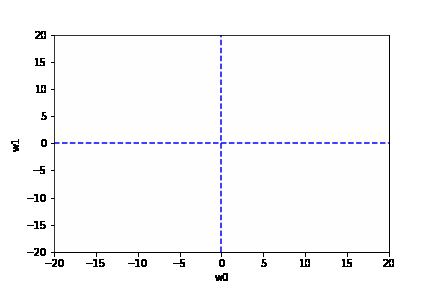
学習率は大きすぎても、小さすぎても駄目です。{(w0, w1) = (0, 0) に近づきません}
適切な学習率を設定した場合は、以下のように目標とする損失関数にたどり着けます。
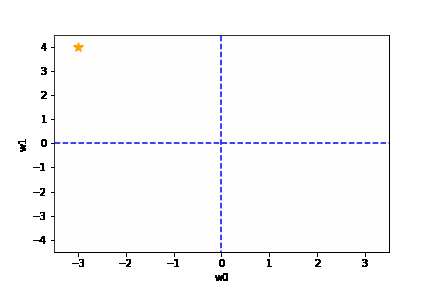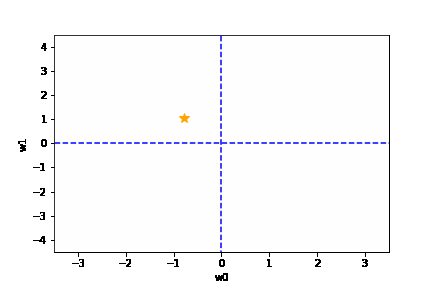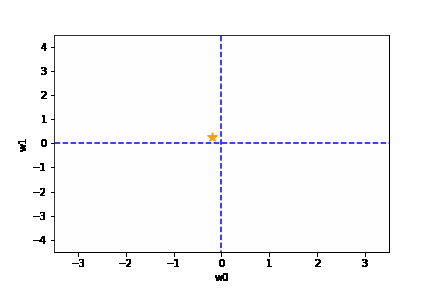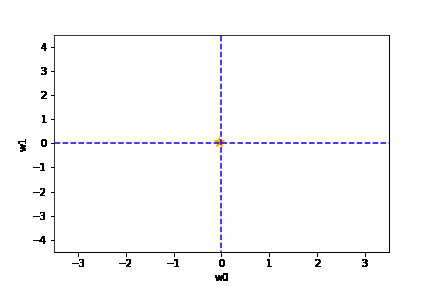
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch04/gradient_method.py
確率的勾配法の実装
これまで学んだ確率的勾配法 (SGD) を実際に実装したものが以下のソースコードとなります。
train acc が訓練データの予測正解率、test acc がテストデータ (まだ学習したことの無いデータ)の予測正解率です。
関連記事
ディープラーニング入門記事の続きは以下のとおりです。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク ←イマココ
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)