初めに
本記事は機械学習で利用するアルゴリズムの k-means法について記載しています。
その他の記事は以下をご覧ください。
■機械学習のアルゴリズム
■ディープラーニング
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
k-means法のアルゴリズム
k-means法のアルゴリズムは以下のとおりです。
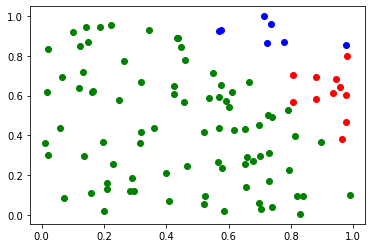
1. 各データにランダムなクラスタを割り当て
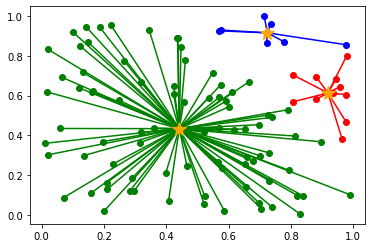
2. クラスタごとに中心を求める
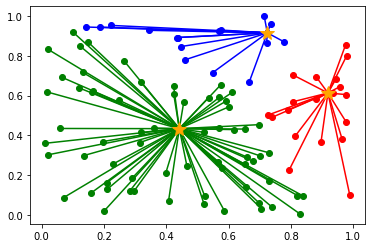
3. 各データを、クラスタ中心が最も近いクラスタに変更
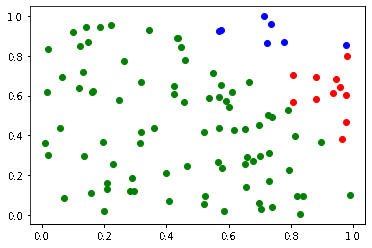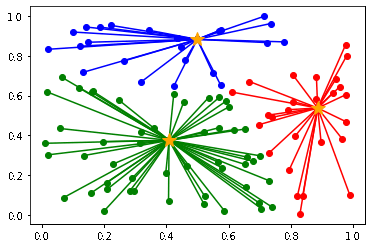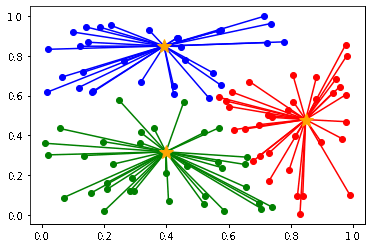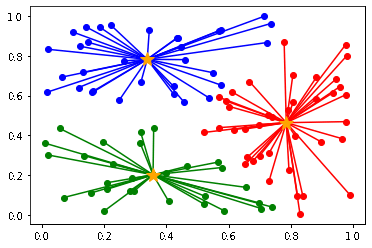
4. 全てのデータのクラスタが変化しなくなるまで、2, 3 を繰り返す
k-means法の欠点
k-means法では、以下のように初期値のクラスタ割り当てに結果が大きく依存します。
- 初期値によって収束する計算量が変わる (最悪の計算量は超多項式)
- 初期値によってクラスタリング結果が異なる (局所的最適解となる)
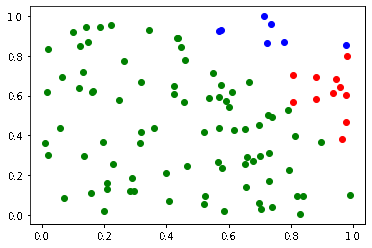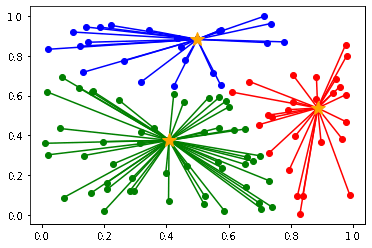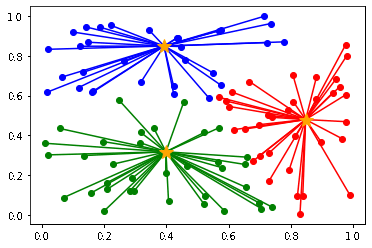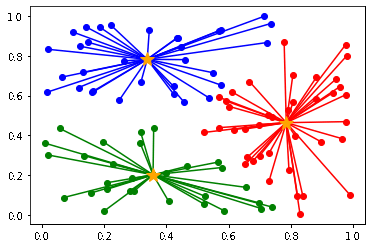
例えば以下のデータを k-means クラスタリングします。
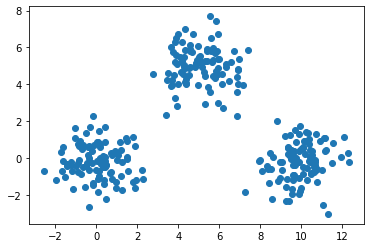
以下のように初期値によって、クラスタリングの結果が異なります。
(収束までの計算量も異なります)


この初期値問題を改善したアルゴリズムとして、k-means++法があります。
k-means++法
k-means++法のアルゴリズム
ここでは、k-means++法のアルゴリズムを説明します。

0. このデータ点を例に k-means++ を説明

1. [データ点] からランダムに1つ選び、[クラスタ中心] とする
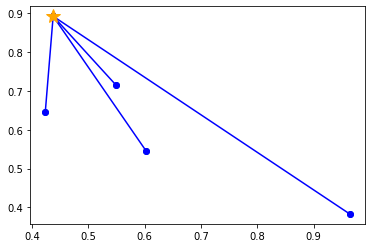
2. [データ点] と [一番近いクラスタ中心] の距離を求める
※複数の [クラスタ中心] が存在する場合は、一番近いものを1つ選択
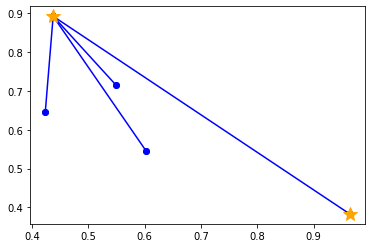
3. 距離が遠いデータ点を選ぶ (確率が高い)
※各データ点が選ばれる確率は以下
$$ (データ点の距離)^2/(各データ点の距離の合計)^2 $$

4. k 個の [クラスタ中心] を選ぶまで、2, 3 を繰り返す
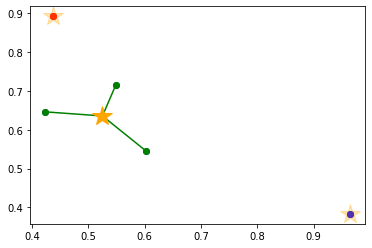
5. k-means 法で k 個のクラスタリングを行う
※ここからの手順は k-means と k-means++ で同じです。
scikit-learn (sklearn) + matplotlib で k-means++ を実装
scikit-learn ライブラリを利用して、さくっと k-means++法を実装します。
なお、可視化しないと結果がわかりにくいので、matplotlib で可視化しています。
from sklearn.cluster import KMeans import numpy as np import matplotlib.pylab as plt data_size = 100 #データ点の数 np.random.seed(0) #データ点の乱数を固定 max_iter = 300 #繰り返しの上限 data = np.random.rand(data_size, 2) #データ点を生成 # k-means km = KMeans(n_clusters=3, max_iter=max_iter) #クラスター数, 繰り返し回数の最大値 clusters_sklearn = km.fit_predict(data) #各データ点がどのクラスター所属するか予測 (クラスター中心が最も近いクラスターを選択) # 可視化処理 for i, row in enumerate(data): if clusters_sklearn[i] == 0: #1つ目のクラスターのデータ点 plt.plot([row[0],km.cluster_centers_[0, 0]], [row[1],km.cluster_centers_[0, 1]], marker='o', color='blue') elif clusters_sklearn[i] ==1: #2つ目のクラスターのデータ点 plt.plot([row[0],km.cluster_centers_[1, 0]], [row[1],km.cluster_centers_[1, 1]], marker='o', color='red') elif clusters_sklearn[i] ==2: #3つ目のクラスターのデータ点 plt.plot([row[0],km.cluster_centers_[2, 0]], [row[1],km.cluster_centers_[2, 1]], marker='o', color='green') # 各クラスター中心点 plt.plot(km.cluster_centers_[0, 0], km.cluster_centers_[0, 1], marker='*', color='orange', markersize=15) plt.plot(km.cluster_centers_[1, 0], km.cluster_centers_[1, 1], marker='*', color='orange', markersize=15) plt.plot(km.cluster_centers_[2, 0], km.cluster_centers_[2, 1], marker='*', color='orange', markersize=15) plt.show()
実行結果は以下のとおりです。
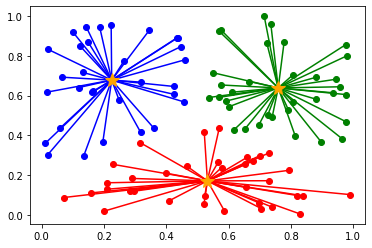
機械学習の関連記事
■機械学習のアルゴリズム
■ディープラーニング
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
参考サイト














































































































