主に分類問題 (グループ分け) の予測に使われます。(回帰問題でも使えます)
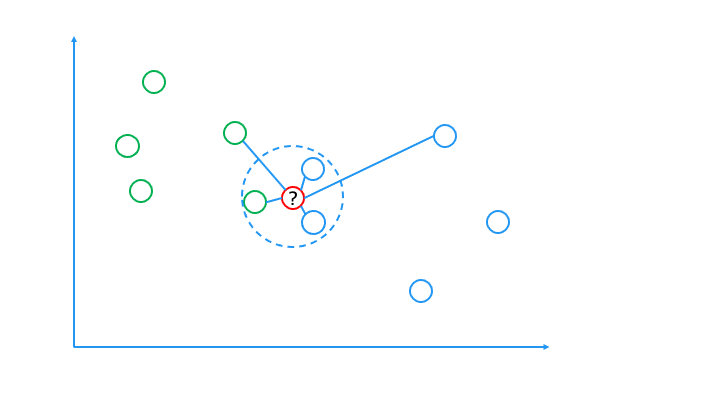
何を持って "近い" とするかは、さまざまな距離の測り方があります。
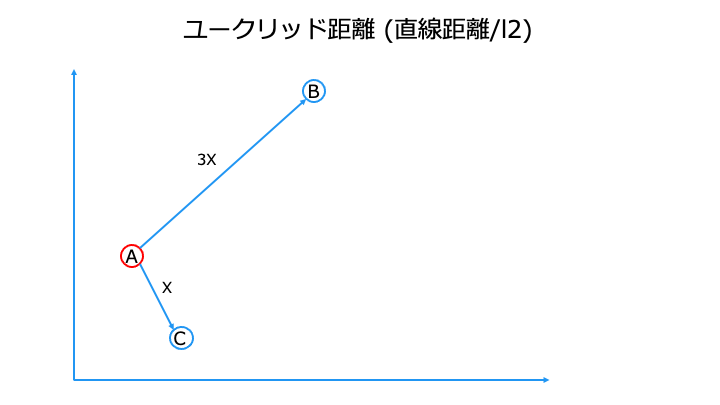
緯度、経度を例にすると、地理的距離が近い方が近くなります
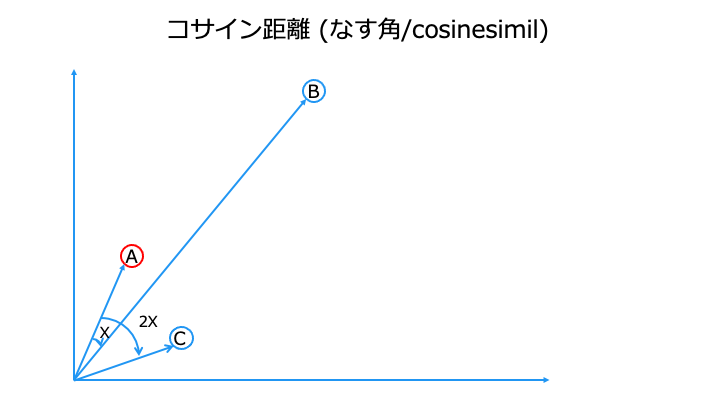
緯度、経度を例にすると、方角が近い方が近くなります。
| 機械学習のアルゴリズム | |||
|---|---|---|---|
| RAG (検索拡張生成) | |||
|---|---|---|---|
k-NN のアルゴリズム
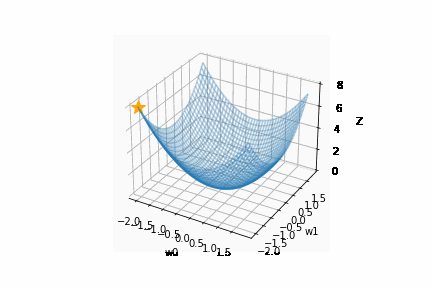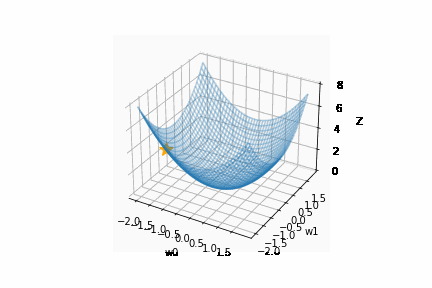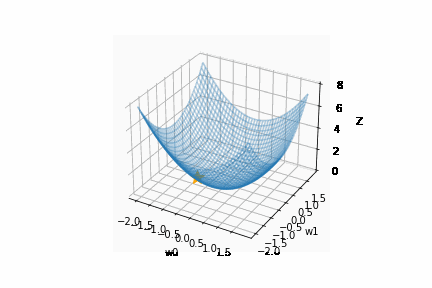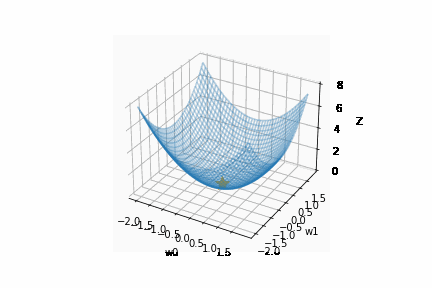
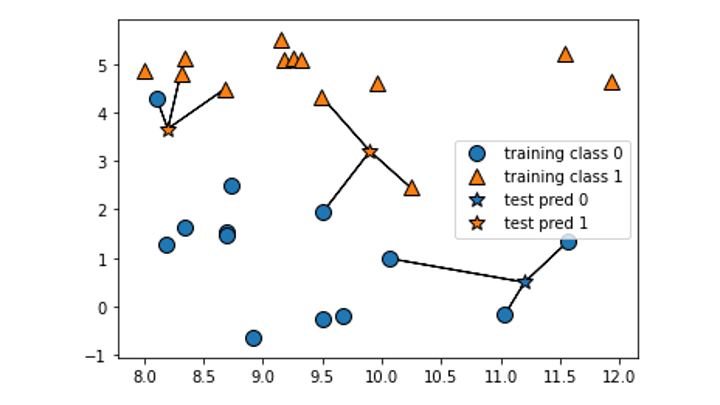
k-NN のアルゴリズムは以下のとおりです。
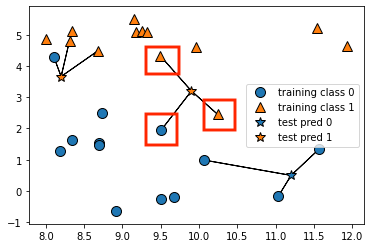
1. 予測するデータから近い順に、k個のデータを選択
予測するデータ = ☆マーク
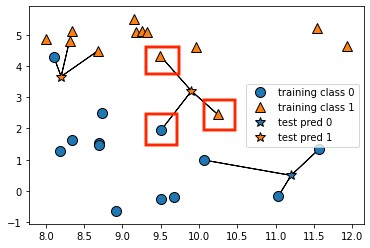
2. 選択したデータのクラスで多数決を取る
オレンジ:2、青:1なので
☆のクラスはオレンジと推測
sklearn で k-NN を実装
ここからは実際に k-NN アルゴリズムで学習して分類機を作成し、予測を行います。
なお、利用するデータセットは以下のとおりです。(2クラス、569人分、30次元のデータ)
| Classes | 2 |
| Samples per class | 212(M),357(B) |
| Samples total | 569 |
| Dimensionality | 30 |
| Features | real, positive |
データセットの確認
k-NN アルゴリズムを利用する前に、今回のデータセットを確認します。
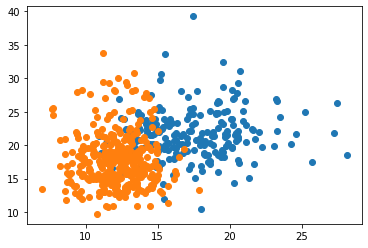
データの散布がわかりやすいように、30次元のうち2次元分を可視化してみます。
(30次元を図にするのは不可能なので)
import matplotlib.pyplot as plt from sklearn.datasets import load_breast_cancer cancer = load_breast_cancer() #データセットを取得 print(cancer.feature_names) #各次元を確認 print(cancer.target) # 正解ラベル plt.scatter(cancer.data[:, 0][cancer.target == 0], cancer.data[:, 1][cancer.target == 0]) #0次元目を可視化 plt.scatter(cancer.data[:, 0][cancer.target == 1], cancer.data[:, 1][cancer.target == 1]) #1次元目を可視化
['mean radius' 'mean texture' 'mean perimeter' 'mean area' (中略) 'worst concave points' 'worst symmetry' 'worst fractal dimension'] [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 (中略) 1 1 1 1 1 1 1 0 0 0 0 0 0 1]
以下の内容が確認できました。
- cancer.data:30次元のデータが569人分存在
- cancer.feature_names:30次元の各次元の名前
- cancer.target:正解ラベル (どちらのクラスか)
python + sklearn で実装
sklearn を利用して、k = 3 で k-NN を利用した分類機を作成します。
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer() #特徴量と正解ラベルを持つデータセットを取得
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, stratify=cancer.target, random_state=0) # 特徴量Xと正解ラベルyを訓練データとテストデータに分ける
clf = KNeighborsClassifier(n_neighbors=3).fit(X_train, y_train) # 訓練データを用いて k-NN アルゴリズムで学習し、分類機を作成
clf.predict(X_test) # 分類機を使って、テストデータを予測する
print(clf.predict(X_test) == y_test) # 予測がどれだけ正解しているか、正解ラベルを使って確認
print("予測精度=", clf.score(X_test, y_test)) # 予測精度
[False True True True True True True True True True True True (中略) True False True True True True True True True True True] 予測精度= 0.916083916083916
k-NN アルゴリズムを利用して、予測精度が 91% の分類機が作成できました。
最後に
関連記事
| 機械学習のアルゴリズム | |||
|---|---|---|---|
| RAG (検索拡張生成) | |||
|---|---|---|---|
| ディープラーニング | ||||
|---|---|---|---|---|
 k-means
k-means KNN
KNN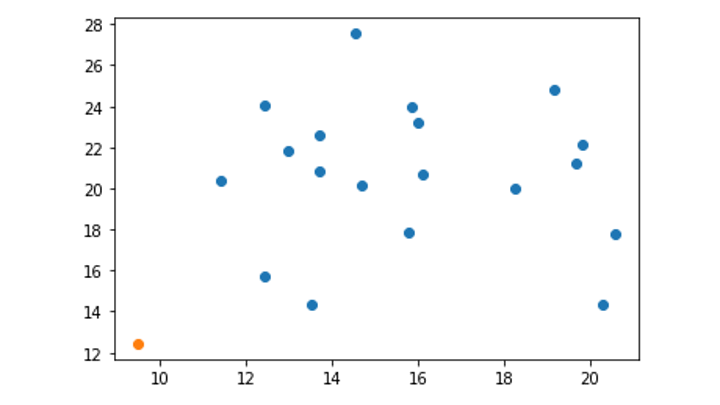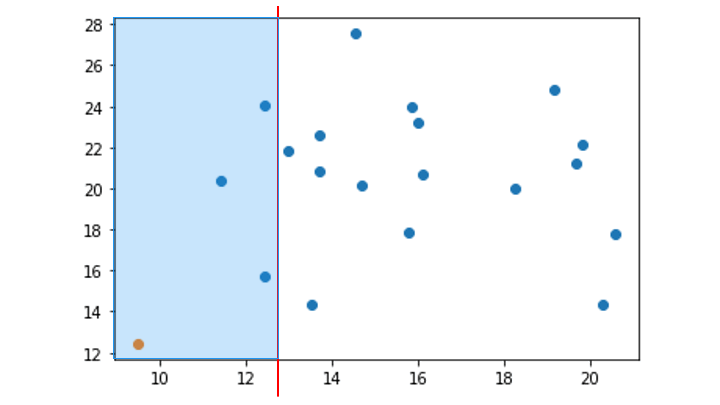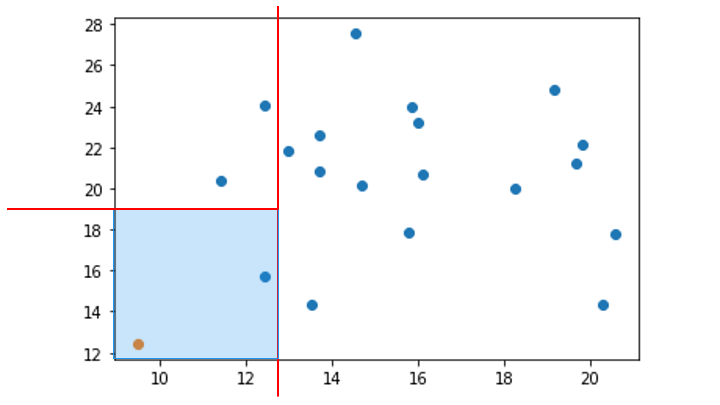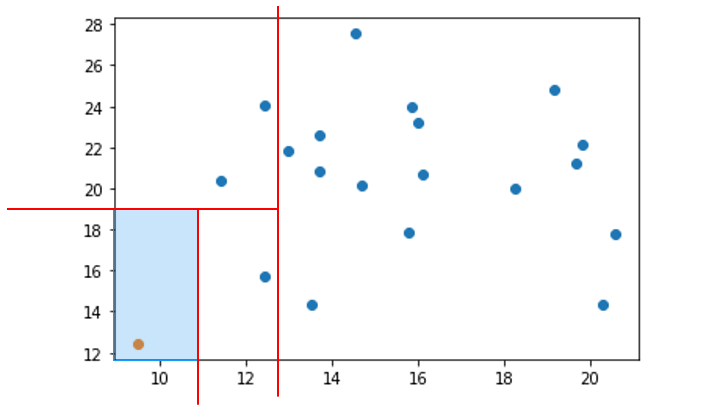 ランダムフォレスト
ランダムフォレスト
 KNN
KNN