本記事は、ディープラーニング入門シリーズの第4回目です。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化 ←イマココ
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
最適化アルゴリズムの一覧と比較
ニューラルネットワークの学習で利用する最適化アルゴリズムには、以下の種類があります。
SGD を表す数式は以下のとおりです。(W は重み、← は代入、ηは学習率、∂L/∂W は勾配)
$$ W ← W - \eta \frac{∂L}{∂W} $$
SGD アルゴリズムについては、以下の記事でより詳しく説明しているのでご覧ください。
SGD の欠点
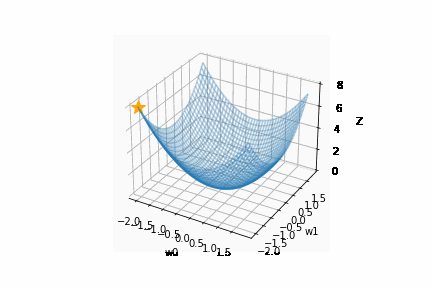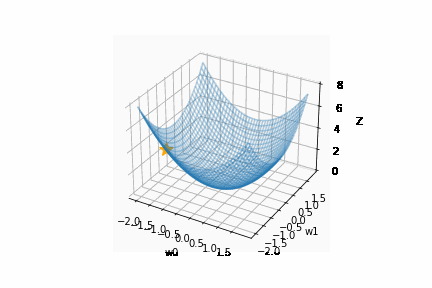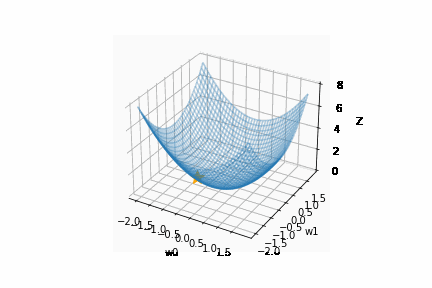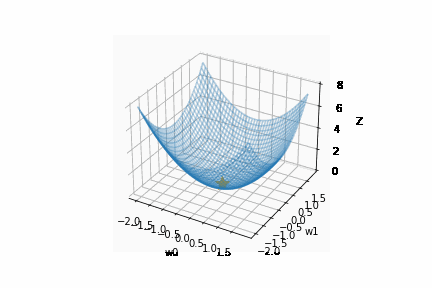
SGD は、関数の変数が均等でない場合は、非効率な探索を行います。
以下のように、x よりも y のほうが f(x, y) の値の変化に大きな影響を与える関数を例に考えます。
$$ f(x, y) = \frac{1}{20}x^2 + y^2 $$
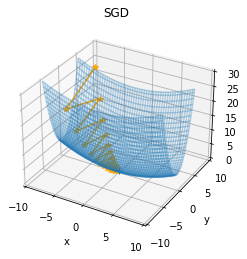
この関数では y = 0 が最小ですが、y 軸方向で発散 (y = 0 を通り過ぎて行ったり来たり) し、非効率な探索をしています。
SGD のこの欠点を解決するために、以下の4つの方法が存在します。
以下の Momentum では、斜面からボールを落とすように徐々に高度が下がっていく様子を確認できます。(SGD と比較して、y 軸で発散する回数が減っています。)
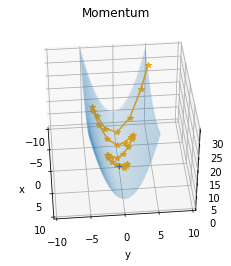
Momentum を表す数式は以下のとおりです。
(v は速度、← は代入、α は 0.0~1.0、ηは学習率、∂L/∂W は勾配、W は重み)
$$ v ← αv - \eta \frac{∂L}{∂W} $$
$$ W ← W + v $$
以下の AdaGrad では、y 軸で発散せずに効率的に学習が行えていることがわかります。
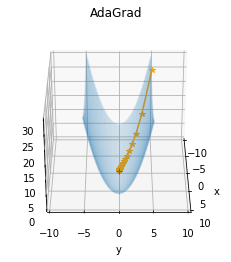
AdaGrad を表す数式は以下のとおりです。
(h は学習率を下げるもの、← は代入、∂L/∂W は勾配、W は重み、ηは学習率)
$$ h ← h + \frac{∂L}{∂W} \otimes \frac{∂L}{∂W}$$
$$ W ← W - \eta \frac{1}{\sqrt{h}} \frac{∂L}{∂W}$$
$$ \otimes は行列の要素ごとに掛け算$$
AdaGrad は学習率が常に小さくなるため、学習初期に大きな更新があったパラメータは、その後ほとんど更新が行われなくなる問題があります。
これを改良するために、RMSprop は AdaGrad と比較して最近の勾配ほど強く影響を受けます。
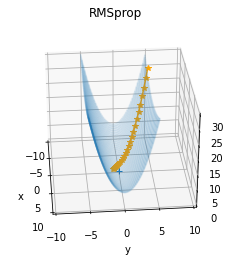
RMSprop を表す数式は以下のとおりです。
(h は学習率を下げる値、← は代入、d は減衰率、∂L/∂W は勾配、W は重み、ηは学習率)
$$ h ← dh $$
$$ h ← h + (1 - d) * \frac{∂L}{∂W} \otimes \frac{∂L}{∂W}$$
$$ W ← W - \eta \frac{1}{\sqrt{h}} \frac{∂L}{∂W}$$
$$ \otimes は行列の要素ごとに掛け算 $$
Adam は Momentum と RMSProp を組み合わせた動きとなっていることがわかります。
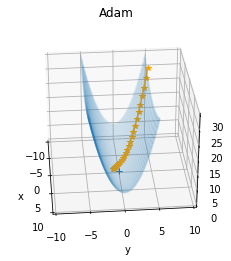
Adam を表す数式は以下のとおりです。
(β1 は 0.9 が標準、β2 は 0.999 が標準、 v は Momentum ベース、h は RMSProp ベース、← は代入、∂L/∂W は勾配、W は重み、ηは学習率)
$$ v ← β_1 v + (1 - β_1) \frac{∂L}{∂W}$$
$$ h ← β_2 h + (1 - β_2) \frac{∂L}{∂W} \otimes \frac{∂L}{∂W} $$
$$ ov ← \frac{v}{(1 - β_1)} $$
$$ oh ← \frac{h}{(1 - β_2)} $$
$$ W ← W - \eta \frac{ov}{\sqrt{oh}}$$
参考数式
https://tech-lab.sios.jp/archives/21823#Adam
https://qiita.com/omiita/items/1735c1d048fe5f611f80#6-rmsprop
重みの初期値
ニューラルネットワークの学習では、重みの初期値が学習結果に大きな影響を与えます。
悪い重みの初期値
一般的に以下の重みの初期値はニューラルネットワークの学習が進まないとされています。
重みの初期値が全て 0 (均一)
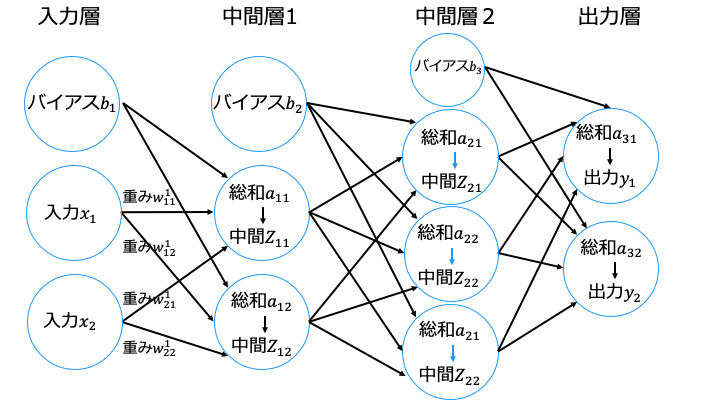
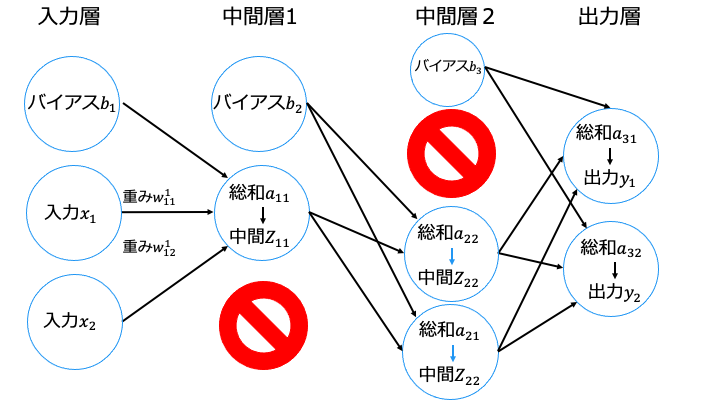
以下の式を見てわかるように、重みの初期値0の場合は 入力 X の値がすべて消えてしまうため正しく学習が行えません。
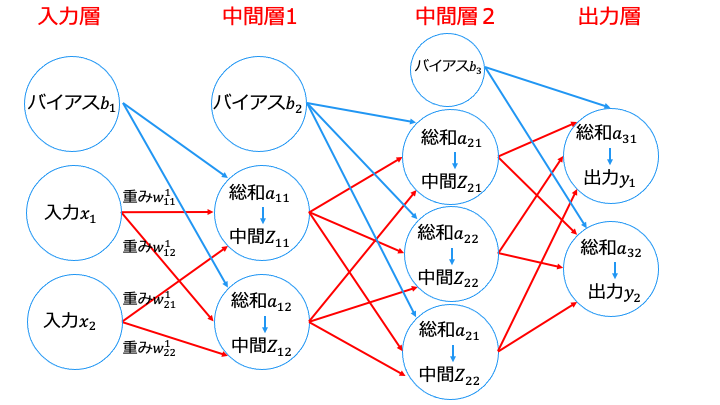
$${A_1 = \left\{\begin{array}{ll}
a_{11} = (b_1+w ^{1}_{11}x_1+w ^{1}_{12}x_1) \\
a_{12} = (b_1+w ^{1}_{21}x_2+w ^{1}_{22}x_2) \\
\end{array} \right. }$$
また、0以外の均一な重みを設定した場合も、同じ比の総和が伝播され層を深くする意味がなくなってしまいます。そのため、均一な重みは推奨されません。
活性化関数の傾きが0に近づく場合
以下の Github にあるニューラルネットワークの学習で、重みの初期値に標準偏差1の正規分布を利用した場合、各中間層の活性化関数 (シグモイド関数) の出力は上記のグラフのようになります。
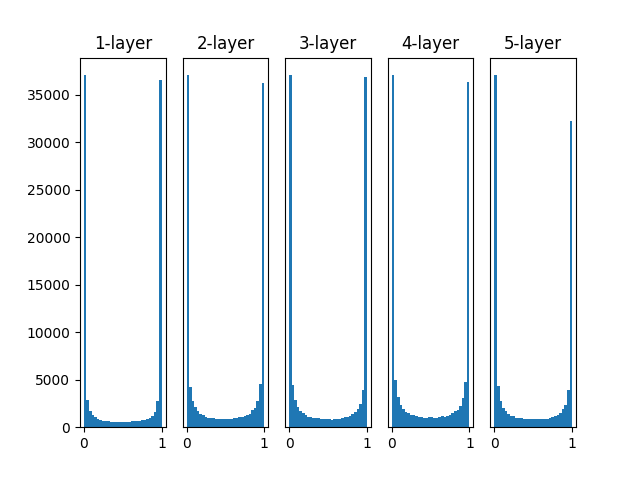
各中間層の活性化関数の結果が0と1に偏っていますが、これは次に紹介する勾配消失という問題が発生します。
シグモイド関数は0と1に近づくほど、傾きが0に近づきます。
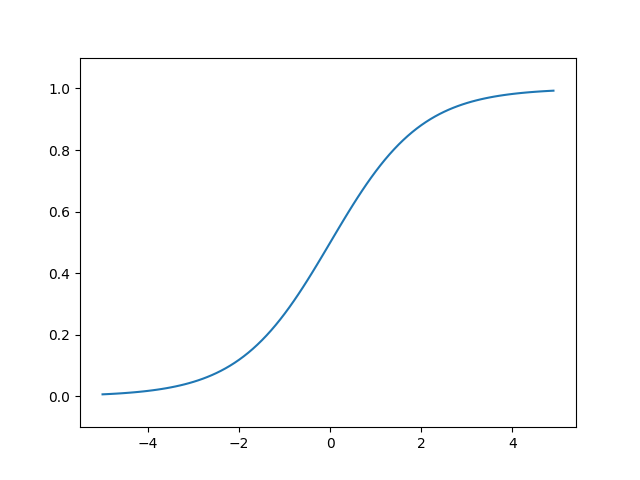
また、層が深くなると勾配を求める際の連鎖律により、傾きの掛け算をする回数が増えます。
そのため、「傾きが0に近く」、「層が深い」ほど勾配が0に近づき、消失します。
(例:1層目 0.001 * 2層目 0.001 * 3層目 0.001 = 勾配 0.000000001)
最適化アルゴリズムの数式を見てわかるように、勾配 (∂L/∂W) が0に近づくと、ニューラルネットワークの学習は進まなくなります。
活性化関数の出力の分布が偏る場合
以下の Github にあるニューラルネットワークの学習で、重みの初期値に標準偏差 0.01 の正規分布を利用した場合、各中間層の活性化関数 (シグモイド関数) の出力は上記のグラフのようになります。
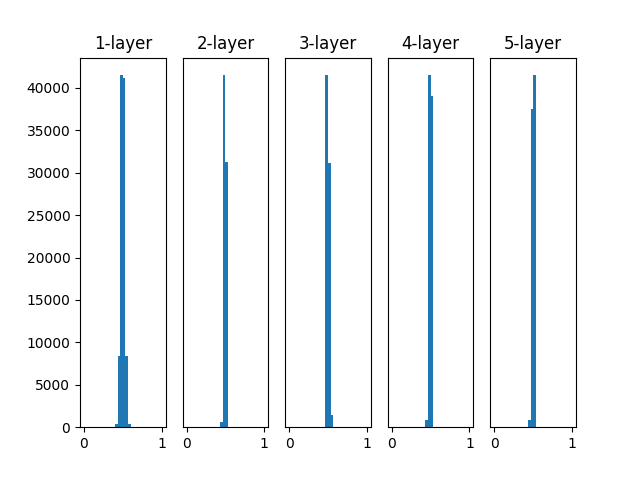
各中間層の活性化関数の出力は 0.5 付近に集中しています。
これは、中間層がほとんど同じ内容しか伝播できないため、入力の違いをあまり表現できていないことを意味します。
良い重みの初期値
悪い重みの初期値の内容から、活性化関数の出力の分布に広がりがあるように、重みの初期値を設定すればよいことがわかります。
一般的に良いとされる、重みの初期値は以下のとおりです。
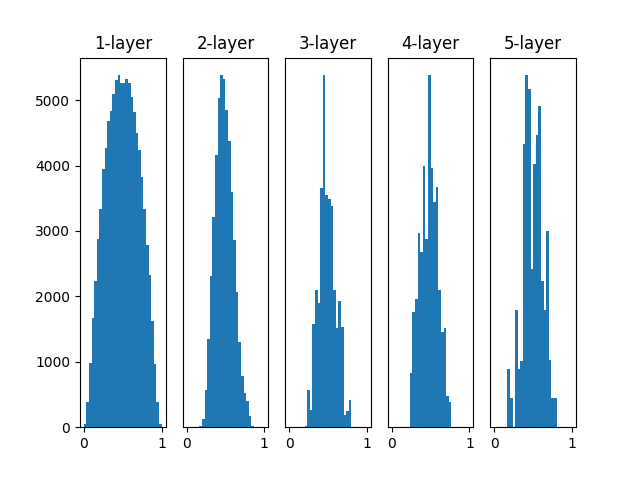
これまでより、出力の結果に広がりがあるため、入力の違いを表現できています。
また、0と1に値が少ないことから、勾配消失の発生を抑えています。
中間層の活性化関数に ReLU を利用する場合、He の初期値を利用します。
重みに各初期値を適用した結果を以下に示します。
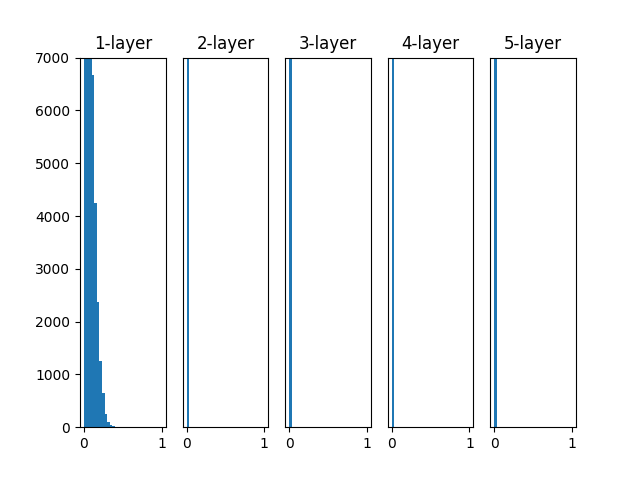
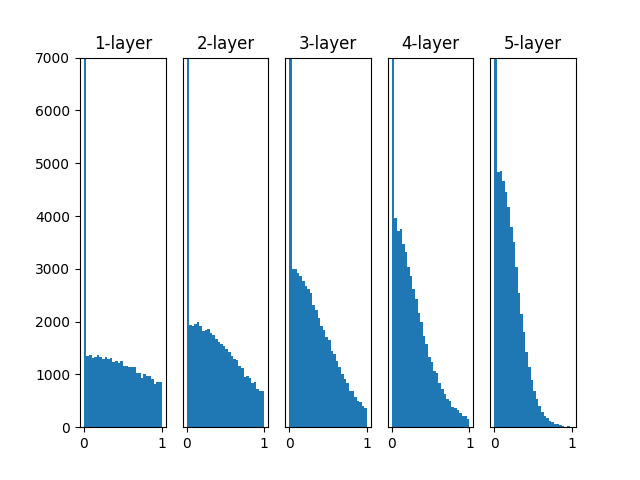
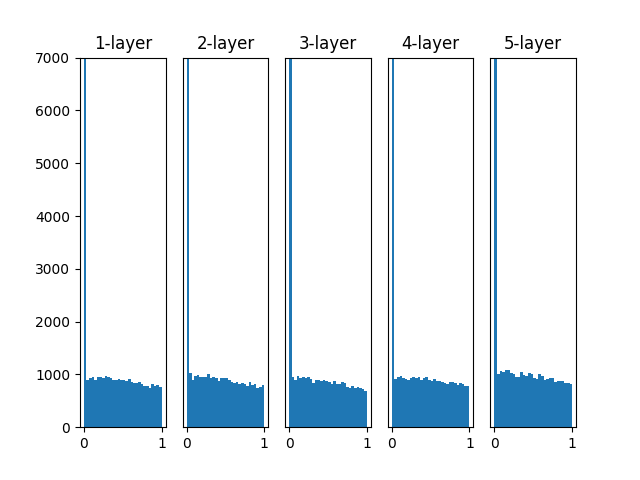
https://github.com/oreilly-japan/deep-learning-from-scratch/blob/master/ch06/weight_init_activation_histogram.py より
- 標準偏差 0.01 の正規分布の初期値の場合、0 に集中するため勾配消失が発生します
- Xavier の初期値の場合、層が深くなるにつれ、0 に偏るため表現が偏ったり、勾配消失が発生します
- He の初期値の場合、層が深くなっても分布の偏りがありません。
各重みの初期値でごとに、ニューラルネットワークの学習の進み方を確認してみます。
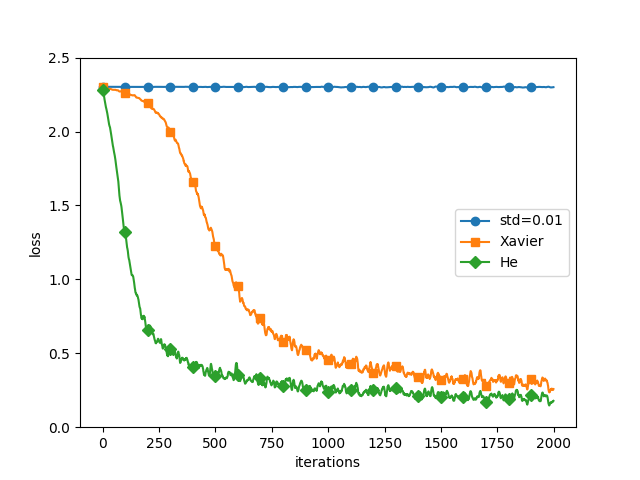
上の図では、損失関数 (loss) が減ると、ニューラルネットワークの学習が進んでいることを表します。
- 標準偏差 0.01 の正規分布の初期値の場合、損失関数がほとんど減っていません
- Xavier の初期値と He の初期値では、He の初期値のほうが学習が早く、予測精度も高いことがわかります。
Batch Normalization とは
「重みの初期値を適切に設定する方法」と「Batch Normalization」を比較すると以下のとおりです。
「重みの初期値を適切に設定する方法」を利用する場合
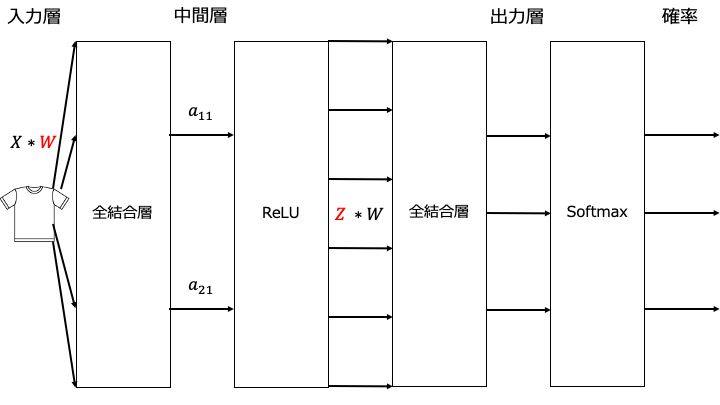
「Batch Normalization」を利用する場合
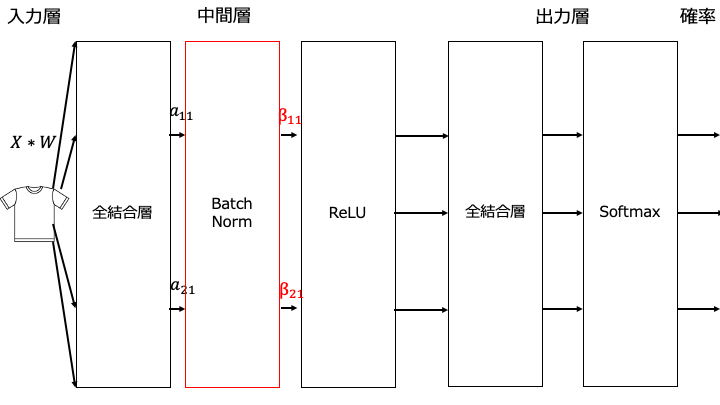
正規化の手順
正規化の手順は以下のとおりです。
$$ 平均 \mu _B ← \frac{1}{m} \sum_{i=1}^{m} x_i $$
$$ 分散 \sigma _B^2 ← \frac{1}{m} \sum_{i=1}^{m} (x_i - \mu _B)^2 $$
$$ 正規化 x_{i}^{'} ← \frac{x_i - \mu _B}{\sqrt{\sigma _B^2 + \epsilon}} $$
※ x は入力、m は入力データの個数、εは 0 で除算することを防ぐための限りなく小さい数
Batch Normalization の数式
Batch Normalization レイヤの処理を数式で表すと以下のとおりです。
$$ y_i = \gamma x _{i}^{'} + \beta $$
※x' は正規化した入力、パラメータ γ = 1, β = 0 (一般的な初期値は左記)
Batch Normalization の効果
Batch Normalization の利点は以下の3つです。
- 学習を早く進行できる (学習率を大きくできる)
- 重みの初期値にそれほど依存しない (Batch Normalization レイヤーで是正する)
- 過学習を抑制
過学習とは
過学習の起きる原因は以下の3つです。
- パラメータを大量に持ち、表現力が高いニューラルネットワークのモデル
- 重みパラメータが大きな値をとる
- 訓練データが少ない
過学習を防ぐ手法は以下の2つがあります。
- Weight decay (荷重減衰)
- Dropout
具体的には損失関数に 1/2λW^2 のノルムを加算します。
(λはペナルティの大きさを調整するパラメータ。勾配には、微分した λW を加算)
なお、加算するノルムによって、以下のように呼ばれます。
$$ L1 ノルム = |w_{1}^{2}|+ |w_{2}^{2}|+・・・+ |w_{n}^{2}| $$
$$ L2 ノルム = \sqrt{w_{1}^{2}+ w_{2}^{2}・・・+ w_{n}^{2}} $$
$$ L \infty ノルム = max|W| (w の絶対値の最大値) $$
Weight decay は実装が簡単ですが、ニューラルネットワークのモデルが複雑になると効果が薄くなります。そこで、Dropout を利用します。
なお、訓練データを流すたびに消去するニューロンを変更します。
ハイパーパラメータの最適化
ハイパーパラメータの例は以下のとおりです。
- 学習率
- ミニバッチサイズ
- ニューラルネットワークの層の数
- 各層のニューロンの数
- Weight decay 係数
重みやバイアスはニューラルネットワークの学習によって自動で取得されるのに対して、ハイパーパラメータは人間が手動で設定します。
なお、「ハイパーパラメータを全通り検証し、予測精度が高いもの選ぶ」のが理想ですが、1回の計算にめちゃくちゃ時間がかかります。そのため、いくつかのハイパーパラメータを試し、予測精度が高いものを選びます。
ハイパーパラメータの決め方には、主に以下の3つの方法があります。
例えば、ハイパーパラメータ「学習率」をランダムに設定し、以下の結果を得たとします。
- 学習率 0.9:ニューラルネットワークの予測精度 90%
- 学習率 0.8:ニューラルネットワークの予測精度 80%
- 学習率 0.7:ニューラルネットワークの予測精度 70%
この場合は学習率 0.9 を採用します。(もしくは学習率をあげれば予測精度が上がりそうなので、学習率0.95 で検証してみる)
初めにランダム検索によりなんとなく良さそうなハイパーパラメータの傾向を調べ、その値に対してグリッド検索を使う方法があります。
砕けた言い方をすると、「確率的に考えて、平均値付近に点が集まる可能性が高いよね。」という考えです。
結局、ガウス過程って何?
https://qiita.com/typecprint/items/2745932fdaf36d763623
任意の点集合x1,...,xNに対するy(x)の同時分布が、ガウス分布に従うもの。
予測精度を出力する関数 f(x) が分かれば、f(x) の値が良くなるようにハイパーパラメータ x を決定できます。
ベイズ最適化の流れ (活用と探索による自動調整)
※超雰囲気解説です。厳密には参考資料を読んでください。
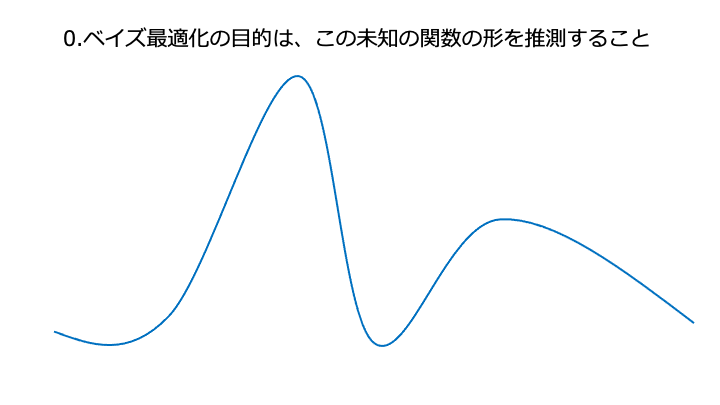
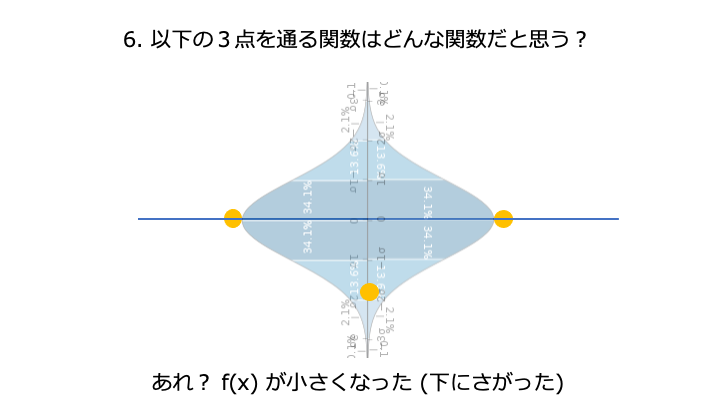
上記の予測精度を出力する関数の、一番高いところを求めたい。
(予測精度を出力する関数に損失関数を使う場合は、一番低いところ)

xは横軸、f(x) は縦軸
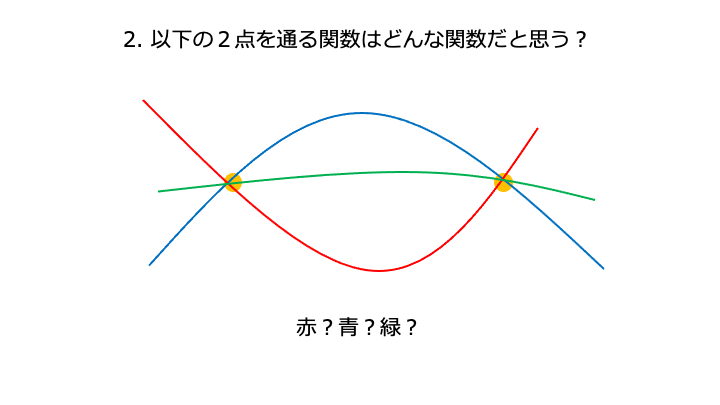
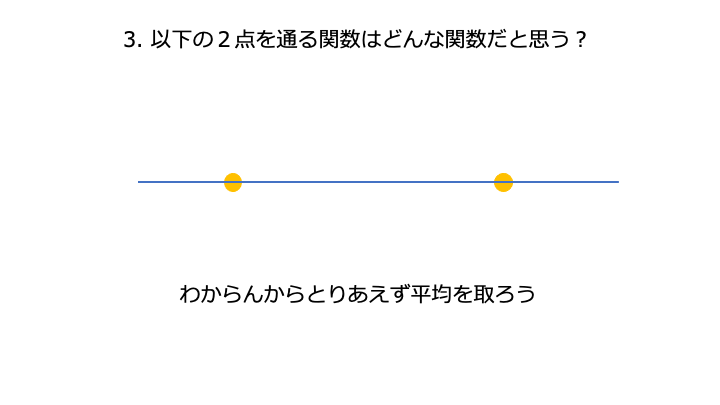
[今までの経験 (平均) からある程度予想できること]
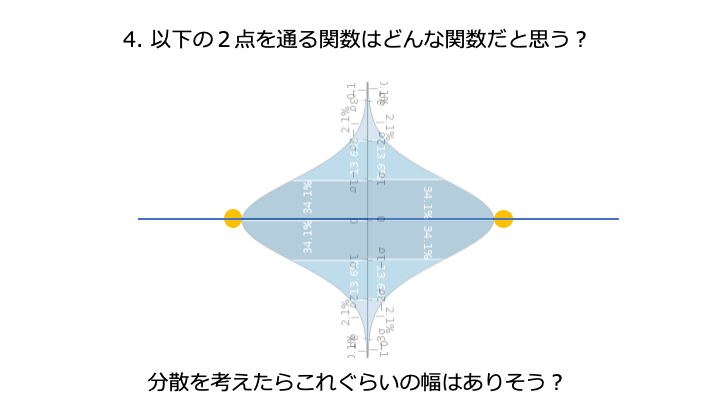
[経験のないこと (実際にどれぐらい分散するか) に挑戦して知識 (結果) を得ること]
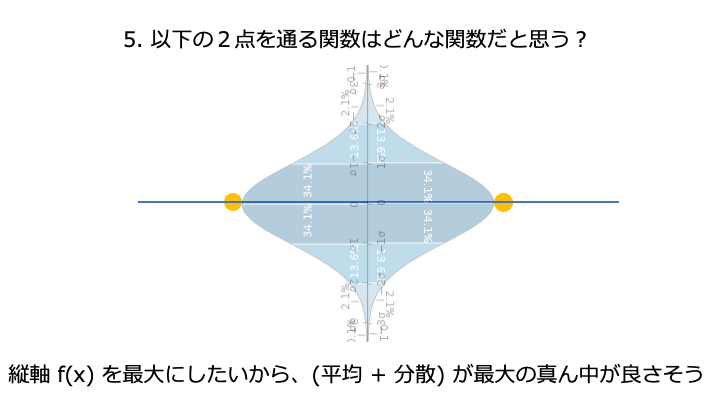
分散 + 平均を acquisition function と呼びます。acquisition function は色んな種類があります。
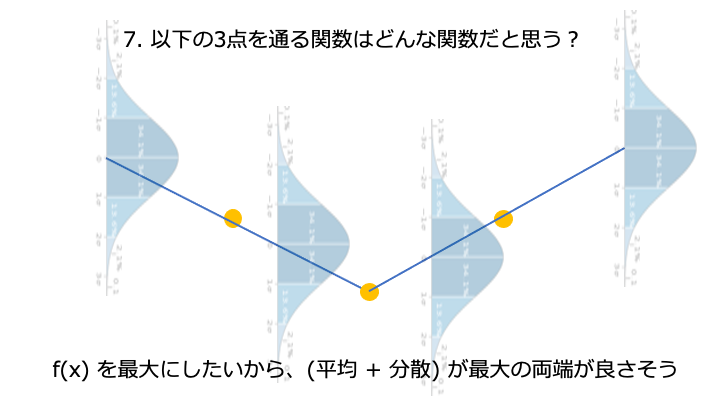
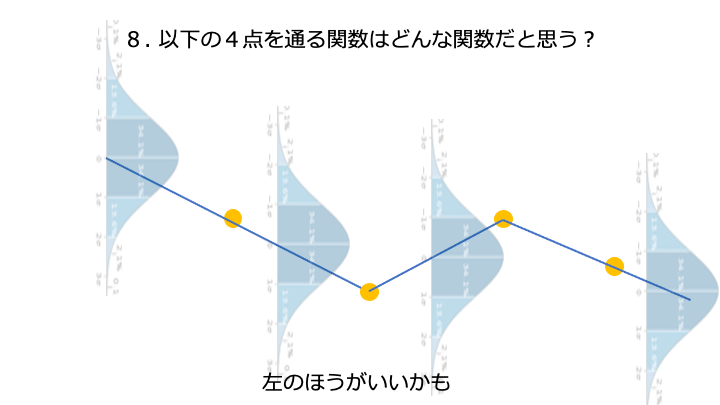
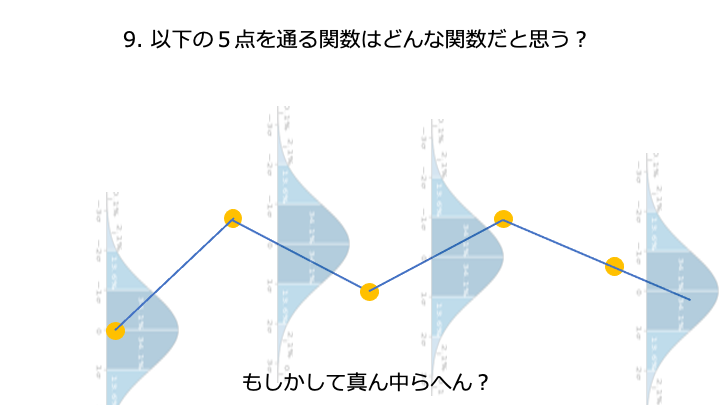
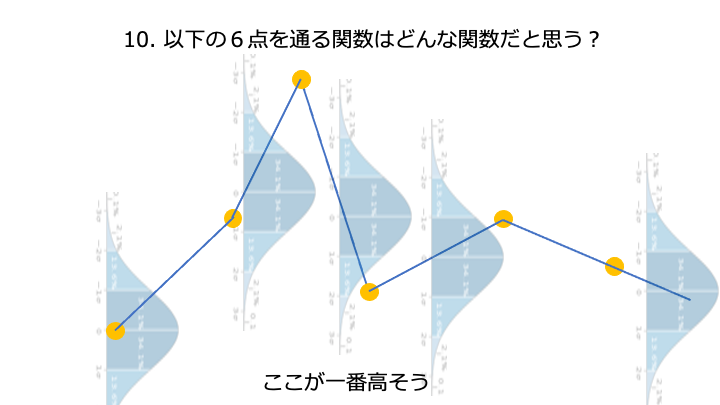
ここが一番高そうです。
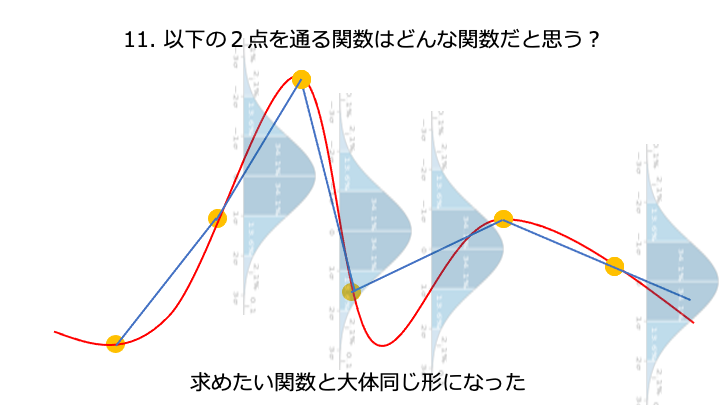
「真の予測精度を出力する関数」と「ベイズ最適化で推測した予測精度を出力する関数」がだいたい同じとなり、高い予測精度を持つハイパーパラメータ x6 が求められました。
関連記事
ディープラーニング入門記事の続きは以下のとおりです。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化 ←イマココ
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN)
参考資料