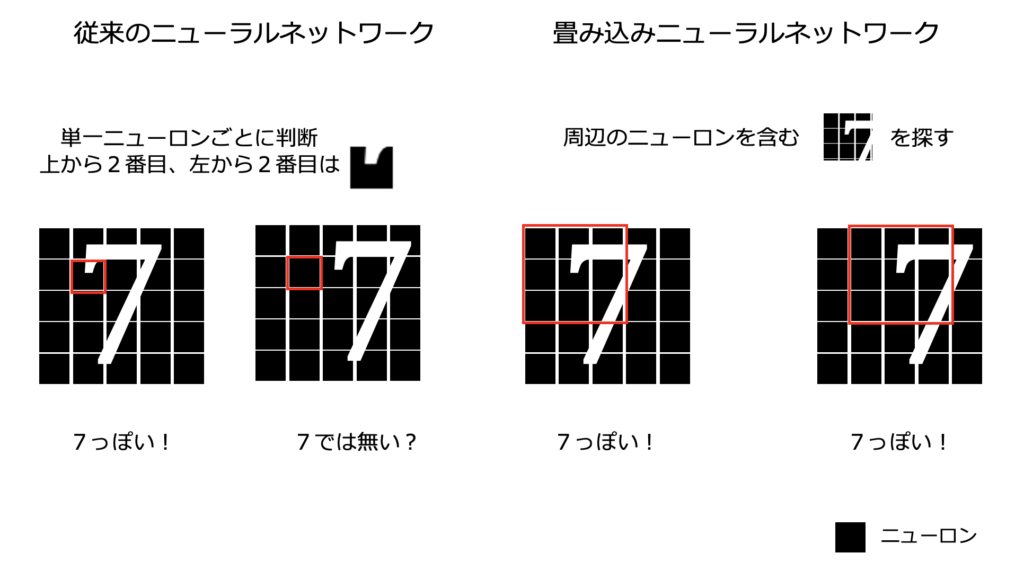
畳み込みニューラルネットワークとは、周辺のニューロンの特徴をまとめて抽出し、データの形状を捉えるニューラルネットワークです。
| ディープラーニング | ||||
|---|---|---|---|---|
従来のニューラルネットワークと CNN の違い
畳み込みニューラルネットワークは、中間層で「全結合層 (Affine)」の代わりに、「畳み込み層 (Convolution)」と「プーリング層 (Pooling)」を利用します。
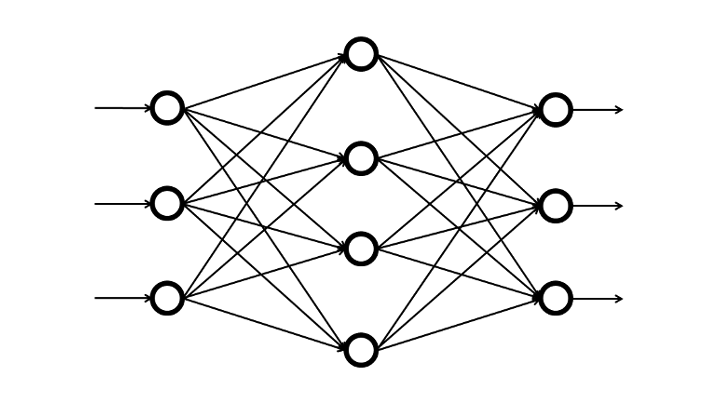
■従来のニューラルネットワーク [全結合層 (Affine) を利用]
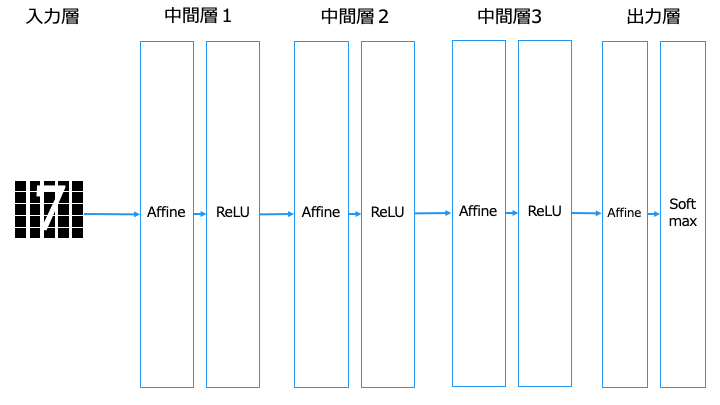
■畳み込みニューラルネットワーク [畳み込み層 (Convolution)、プーリング層 (Pooling) を利用]
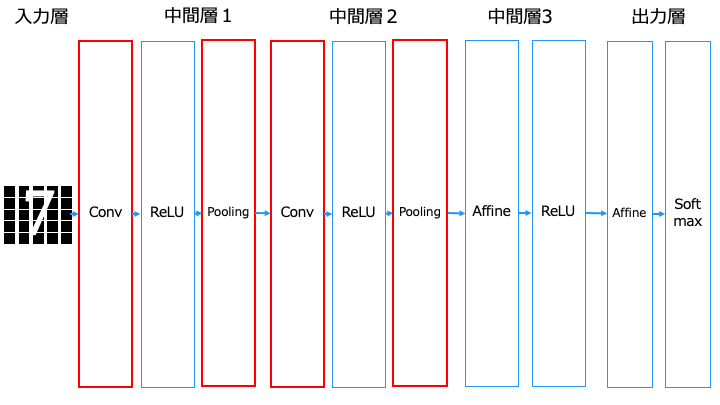
Affine = 全結合層、ReLU = 中間層の活性化関数、Softmax = 出力層の活性化関数
なお、出力層に近い場合、畳み込みニューラルネットワークでも全結合層 (Affine) を利用します。
畳み込み層 (Convolution) とは
畳み込み層では、以下の処理を行います。
- 畳み込み演算(画像処理で言う「フィルタ演算にあたる」)
- バイアスの演算
- パディング
- ストライド
- フィルターを追加
- 次元を追加
畳み込み演算とは
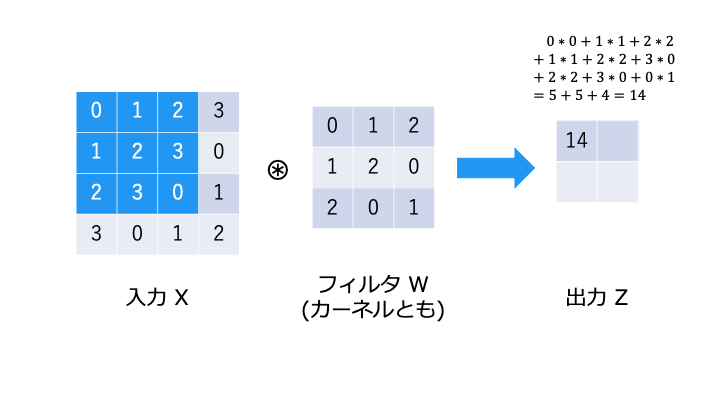
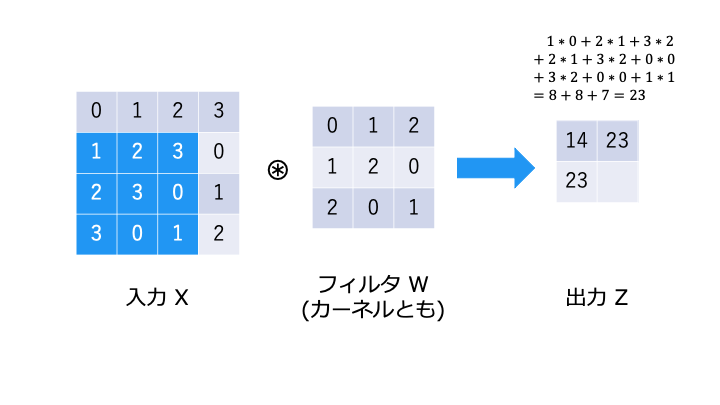
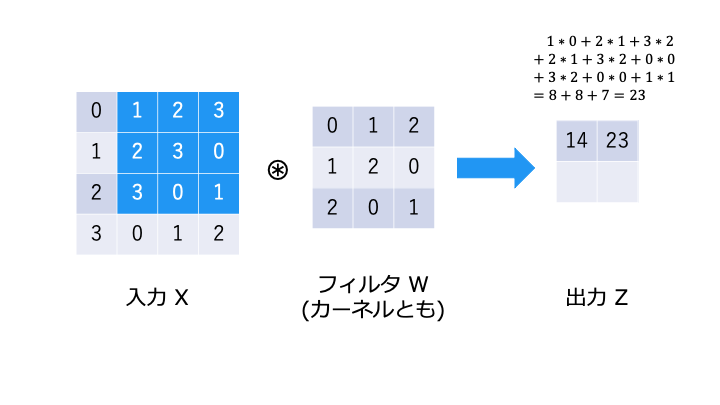
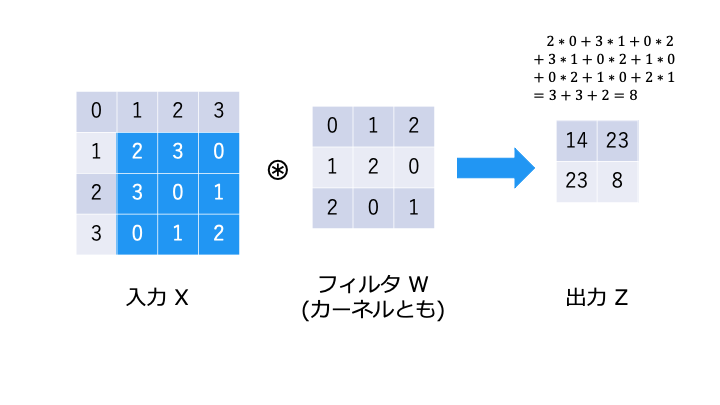
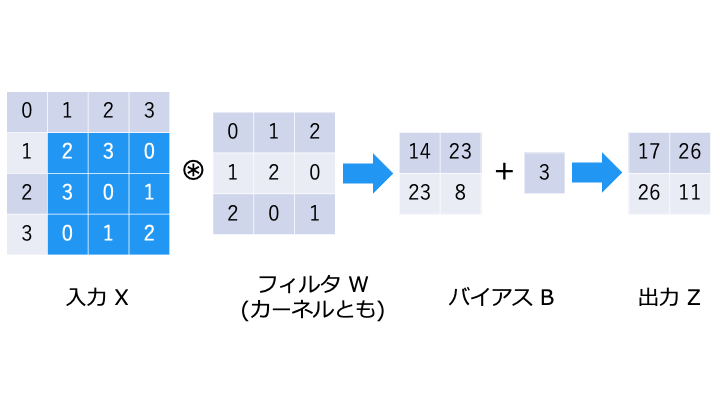
畳み込み演算は以下のような演算です。フィルタが重み W に相当します。
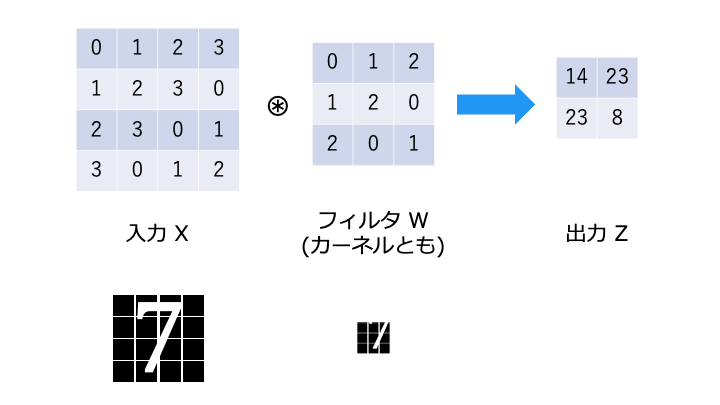
畳み込み演算では、以下のようにフィルタと対応する要素を乗算し、その和を求めます。(積和演算)
バイアスの演算
畳み込みニューラルネットワークでは、以下のようにバイアス B を演算します。
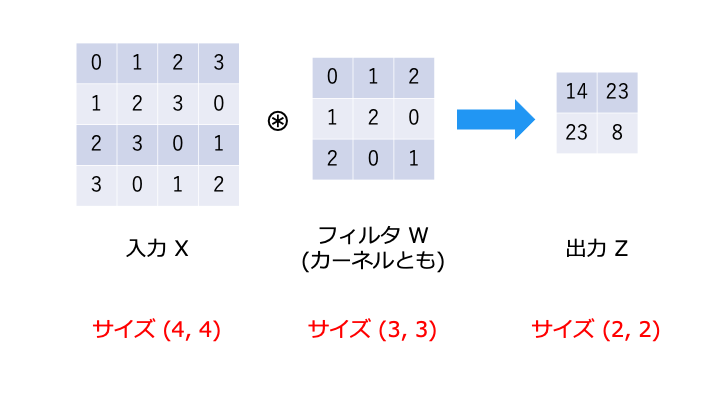
畳み込み演算を行うと、出力のサイズがどんどん小さくなってしまい、最後は畳み込み演算ができなくなってしまいます。
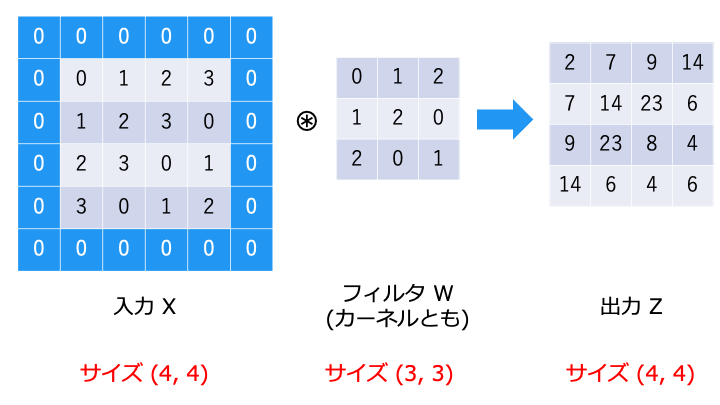
そこで、入力の周囲を0で埋めることで、出力のサイズを調整します。
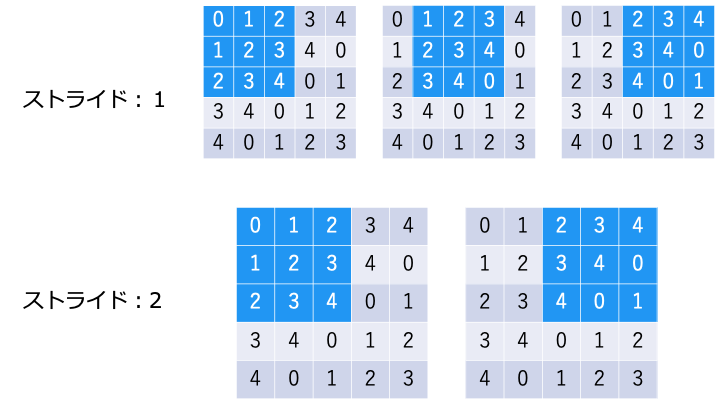
スライドが大きくなると、出力は小さくなります。
- スライド:1 → 出力 (3,3)
- スライド:2 → 出力 (2,2)
フィルターを追加
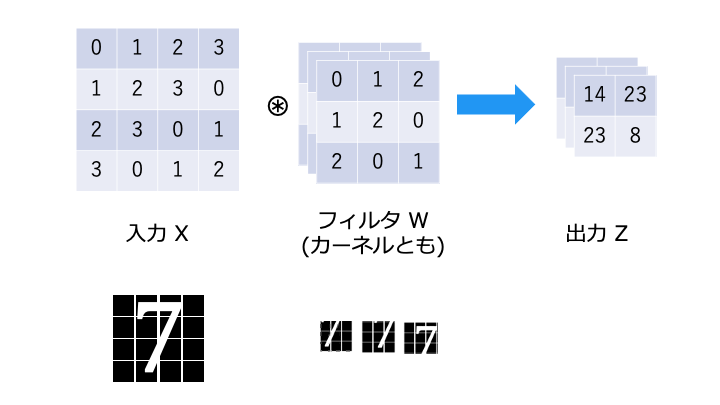
1入力に対して、3つのフィルターでそれぞれ畳み込み演算を行い、3つの出力を得ます。
通常、画像はさまざまな直線・曲線などが組み合わさって構成されるので、1つのフィルタを用いて判別するよりも、複数のフィルタを組み合わせて判別したほうが、識別性能が上がりやすい。
https://www.imagazine.co.jp/%E7%95%B3%E3%81%BF%E8%BE%BC%E3%81%BF%E3%83%8D%E3%83%83%E3%83%88%E3%83%AF%E3%83%BC%E3%82%AF%E3%81%AE%E3%80%8C%E5%9F%BA%E7%A4%8E%E3%81%AE%E5%9F%BA%E7%A4%8E%E3%80%8D%E3%82%92%E7%90%86%E8%A7%A3%E3%81%99/
次元を追加 (カラーの画像認識)
画像の「縦」と「横」の2次元から、「色 (チャンネル)」を追加した3次元を例に見ていきます。
今回、色の表現方法はRGB(Red, Green, Blue)を利用します。
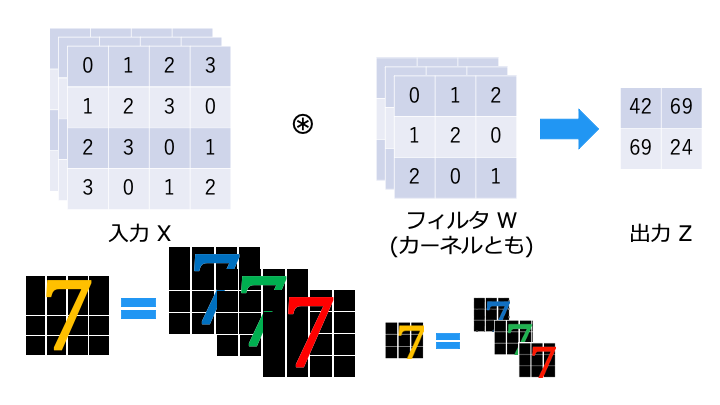
「1入力、1フィルター (1枚のオレンジの7)」です。「色 (チャンネル) = Z 軸方向」に要素を分解してるだけです
入力 X とフィルタ W の要素ごとに畳み込み演算を行い、3つの演算結果 (赤・緑・青) を合計したものが出力となります。
(元々1枚の画像を3つの RGB に分けて計算しただけなので、最後は合計して1枚に戻します。)
畳み込み演算を Python で実装
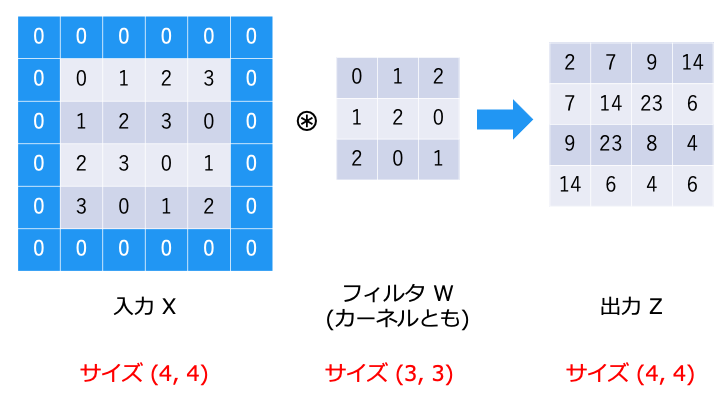
上記の畳み込み演算を実装した結果が以下のとおりです。(im2col の実装はこちら)
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : (データ数, チャンネル, 高さ, 幅)の4次元配列からなる入力データ
filter_h : フィルターの高さ
filter_w : フィルターの幅
stride : ストライド
pad : パディング
Returns
-------
col : 2次元配列
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
input = np.array([[[[0,1,2,3],[1,2,3,0],[2,3,0,1],[3,0,1,2]]]]) #入力 X
filter = np.array([[0,1,2],[1,2,0],[2,0,1]]) #フィルタ W
input_col = im2col(input,3,3,1,1) #引数の詳細はim2col 参照
filter_col = filter.reshape(1, -1).T
output = np.dot(input_col,filter_col) #出力 Z
print(output.reshape(4,4)) #出力Z の形
プーリング層 (Pooling)
今回はプーリング層でよく利用される、Max プーリングについて説明します。
なお、「プーリング」とは、画像処理で言う「ダウンサンプリング」にあたります。
Max プーリングはプーリングウィンドウ (ここでは出力) のうち、最も値の大きいものを選択します。
これは、フィルタに一致するニューロンが最も発火しやすい (高い値となる) からです。
(言い換えると、フィルタに一致する要素があるか無いかを見たいので、一番高い値以外は要らない)
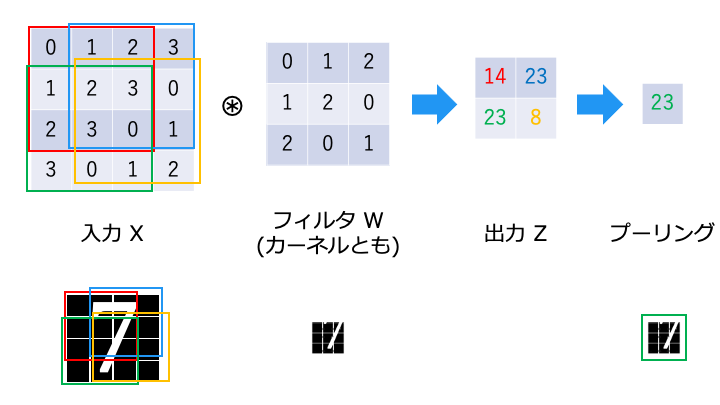
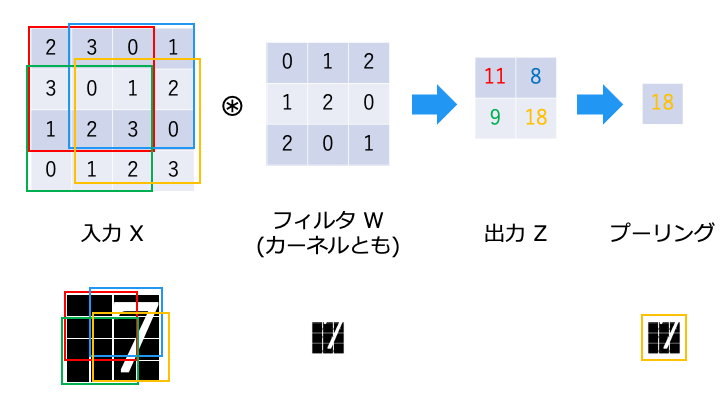
Max プーリングにより、フィルタの位置ズレを吸収し、「7」を検出できていることがわかります。
CNN アーキテクチャの種類
CNN アーキテクチャについて、改良の歴史順に紹介します。
LeNet in 1998
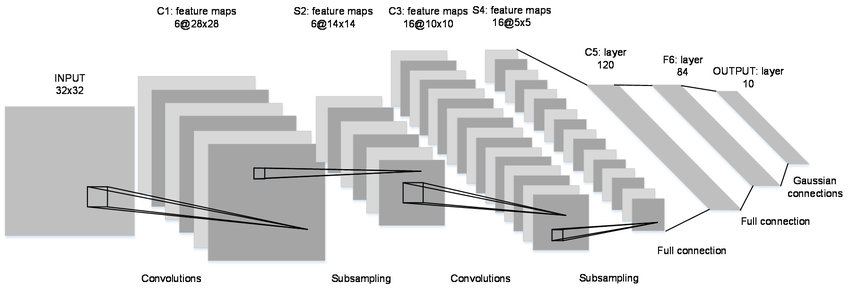
Subsampling がプーリングに相当します。
LeNet は以下の7層から構成されます。
- 畳み込み演算層 (Convolutions + sigmoid 関数) を1層
- サブサンプリング層 Subsampling (プーリングに相当) を1層
- 畳み込み演算層 (Convolutions + sigmoid 関数) を1層
- サブサンプリング層 Subsampling (プーリングに相当) を1層
- 中間層 (全結合層 + sigmoid) を2層
- 出力層 (全結合層 + Softmax) を1層
AlexNet in 2012
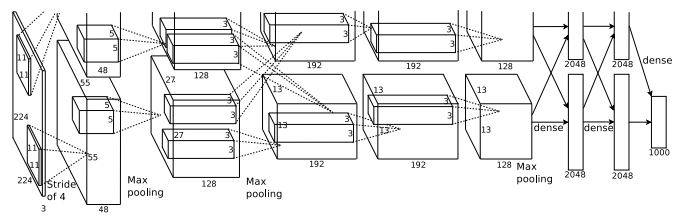
MATLAB では入力を 227 * 227 としている
上下2つに分かれている理由は、当時の GPU では1枚に全てのデータが載らなかったからです。
AlexNet は以下の8層から構成されます。
- 畳み込み演算層 (Convolutions + ReLU + Max Pooling) で5層
- 中間層 (全結合層 + ReLU + Dropout) を2層
- 出力層 (全結合層 + Softmax) を1層
VGG in 2014
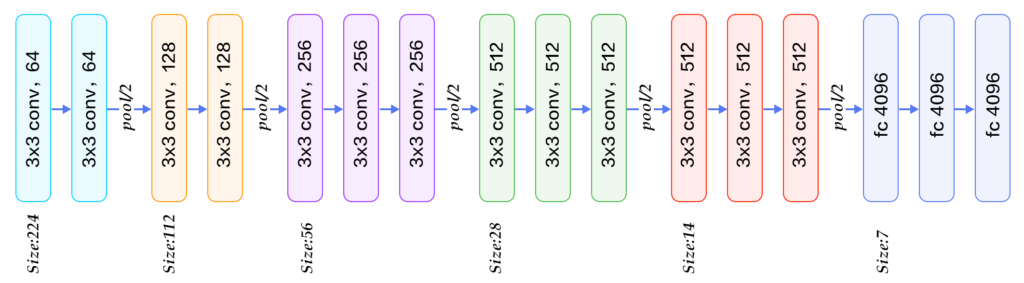
詳細:https://qiita.com/mhiro216/items/e54c2ff204512d877f98
Convolutions (畳み込み演算) を連続で行うことでフィルターサイズを小さくする手法です。
VGG は以下の計 16 層から構成されます。(VGG-16 の場合)
- 畳み込み演算層 ( (Convolutions + ReLU) * 2 + Max Pooling) を2回で4層
- 畳み込み演算層 ( (Convolutions + ReLU) * 3 + Max Pooling) を3回で9層
- 中間層 (全結合層 + ReLU + Dropout) を2層
- 出力層 (全結合層 + Softmax) を1層
なお、各処理の詳細は以下のとおりです。
- Convolutions のパディングは (1, 1) なので出力のサイズは同じ (64→64, ... ,512→512→512)
- Convolutions フィルター数の増加により、チャンネルの次元を増加 (64→128...→512)
- Max Pooling (= ストライド2) により、出力のサイズを半分に (224→112...→7)
AlexNet のフィルター (11, 11) と比較して、VGG のフィルターは (3, 3) なので、少ないハイパーパラメータで学習可能です。
GoogLeNet in 2014
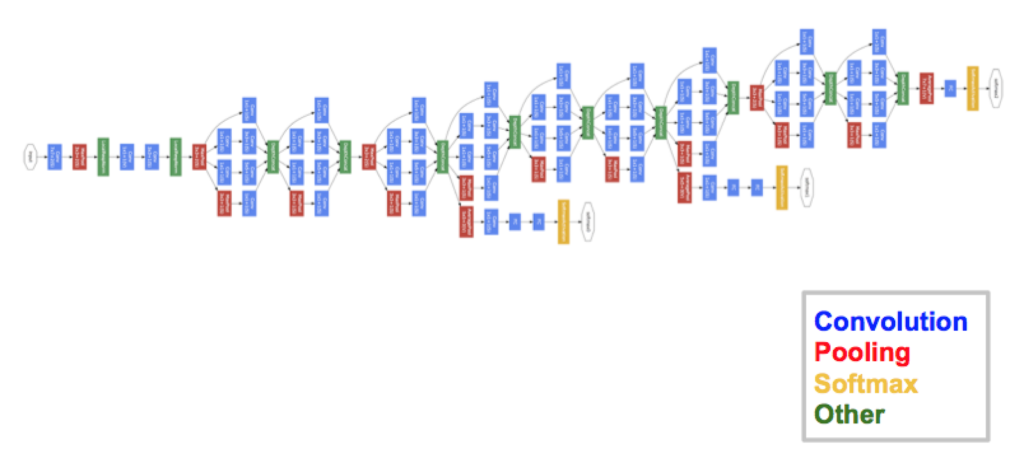
GoogLeNet の最大の特徴は、サイズの異なるフィルター + Max Pooling の結果を結合する「インセプション構造」を持つことです。
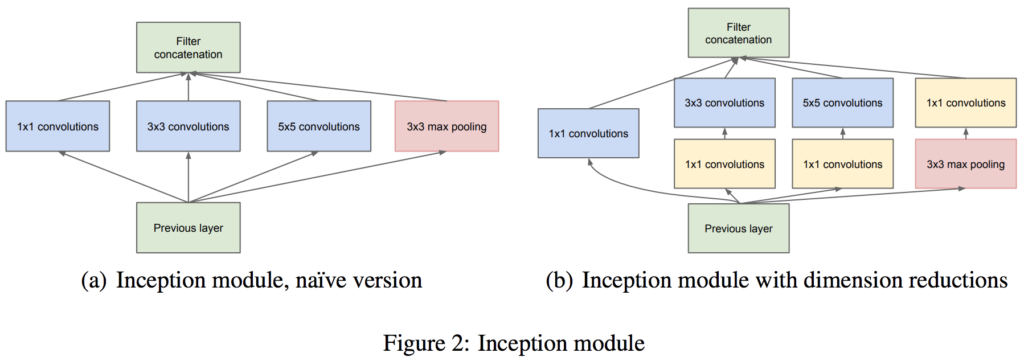
上記の図 (b) では、すべての要素に (1, 1) のフィルターを適用していますが、これはチャネル方向の次元を減らすためです。これにより、ハイパーパラメータの数を削減したり、処理を高速化可能です。
なお、インセプション構造を利用するモチベーションは以下のサイトにわかりやすく解説されています。
2013-2014 年当時、層を深くしたり、各層に存在しているユニットの数を増やしたりすることで、分類の性能が上がることが知られ始めた。しかし、少ないデータの中で、層数やユニット数を増やすことで、過学習を起こしてしまう。そこで、開発者らは Inception と呼ばれるモジュールを作り、その Inception モジュールを重ねていくことで、層を深くすることができた。
これまでのアーキテクチャは、畳み込み層を順列に繋げていた。このため、畳み込み層が深くなるにつれ、画像サイズが小さくなっていき、層を深くすることができなかった。これに対して、GoogLeNet では、1 つの入力画像に対して、複数の畳み込み層(1×1, 3×3, 5×5)を並列に適用し、それぞれの畳み込み計算の結果を最後に連結している。この一連の作業をモジュールとしてまとめられ、Inception モジュールと呼ばれている。
https://axa.biopapyrus.jp/deep-learning/cnn/image-classification/googlenet.html
ResNet in 2015
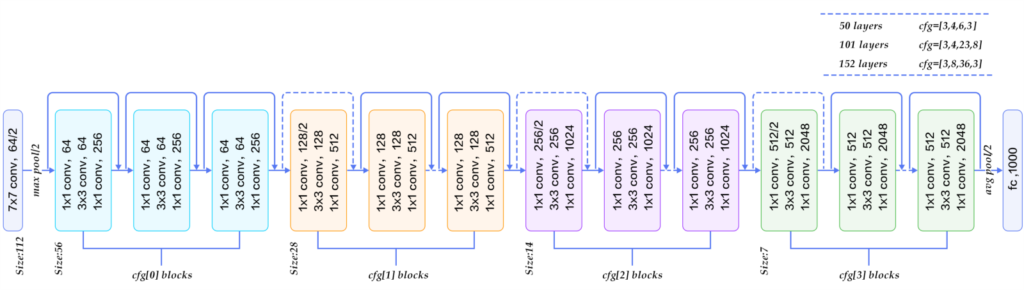
詳細:https://qiita.com/kenmaro/items/008051dae0bf0ad718cb
ResNet では、Convolutions 処理をスキップ可能な「スキップ構造」を採用しています。
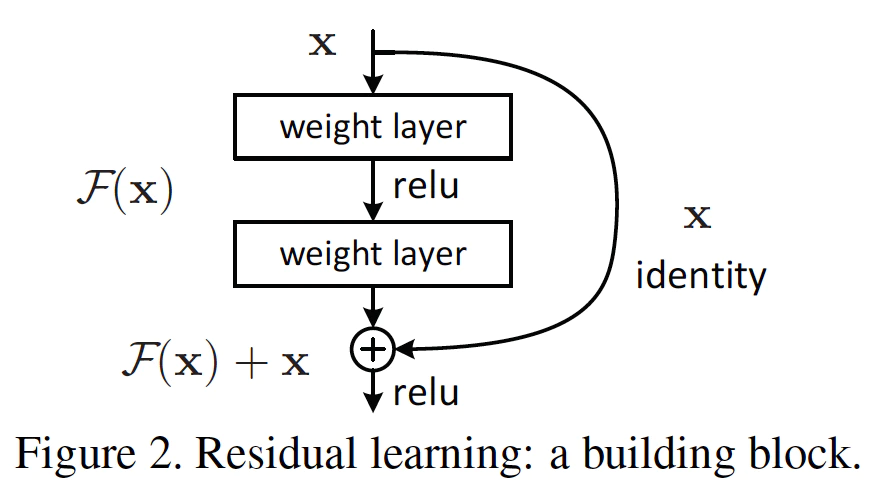
これにより、認識精度が上がる場合に層を深くし、学習がうまく行かない場合に畳み込み演算層をスキップ可能になりました。
ディープラーニング (深層学習)
深層学習として最も普及した手法は、(狭義には4層以上[2][注釈 2]の)多層の人工ニューラルネットワーク(ディープニューラルネットワーク、英: deep neural network; DNN)による機械学習手法である[3]。
https://ja.wikipedia.org/wiki/%E3%83%87%E3%82%A3%E3%83%BC%E3%83%97%E3%83%A9%E3%83%BC%E3%83%8B%E3%83%B3%E3%82%B0
これは、「層を深くすることで error 率が下がる (推論精度が良くなる)」という経験則に基づいています。一方で、理論的にはまだまだわからないことが多いと言われています。
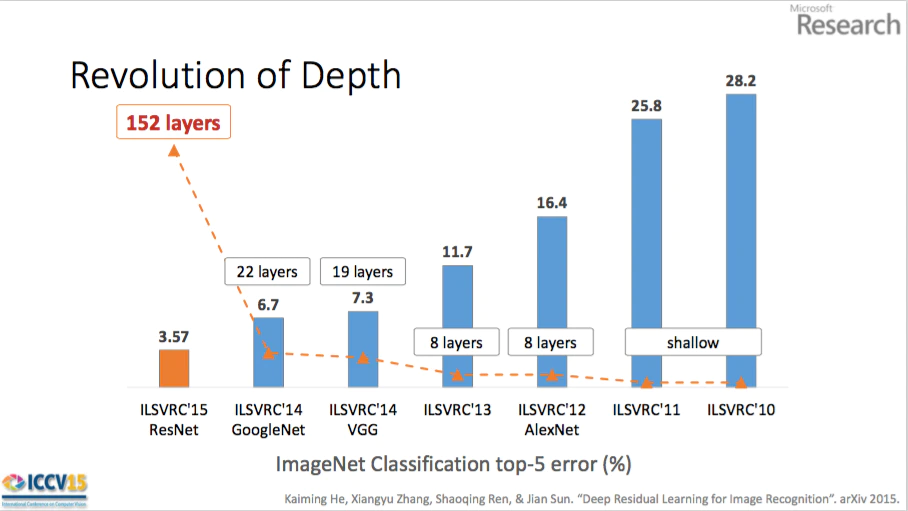
層を深くする利点
層を深くする利点は以下の3つです。
- パラメータの数を削減
- 少ない学習データで学習可能
- 特徴を他のパターン認識に流用可能
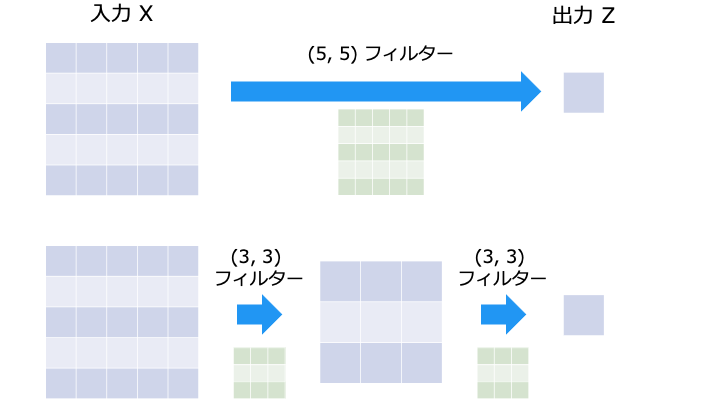
パラメータ数を削減
層を深くした場合は以下のように、少ないパラメータ数で同様以上の表現力を得ることができます。
| フィルターサイズ | 層 | パラメータ数 |
|---|---|---|
| (5, 5) | 1層 | 5 * 5 = 25 |
| (3, 3) | 2層 | 3 * 3 * 2 = 18 |
少ない学習データで学習可能
以下はすべて「7」を表します。
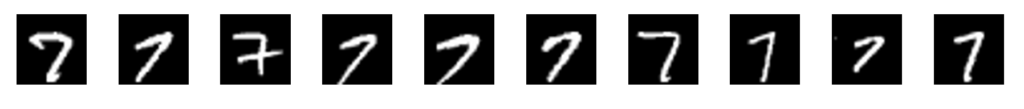
これらを1層で学習する場合は10種類の画像を学習する必要があります。
一方で、層を深く場合は1層目で以下のように4種類のパーツを学習します。
2層目では、1層目のパーツを組み合わせることで「7」を認識します。
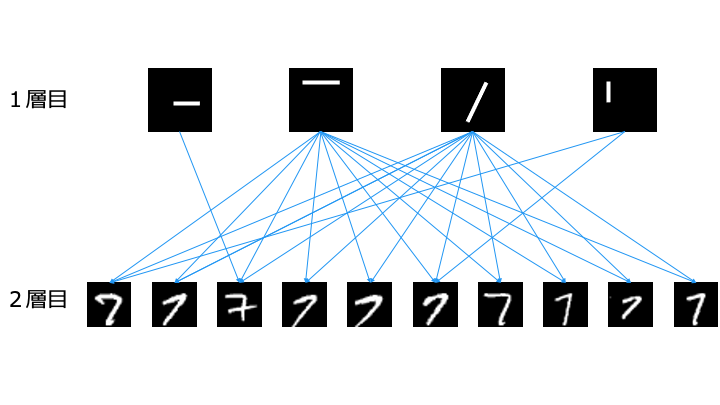
このように、層を深くすると簡単な特徴を学習するだけで良いため、少ないデータでも学習可能となります。
特徴を他のパターン認識に流用可能
層を深くすると、以下のように最小の特徴から学習します。
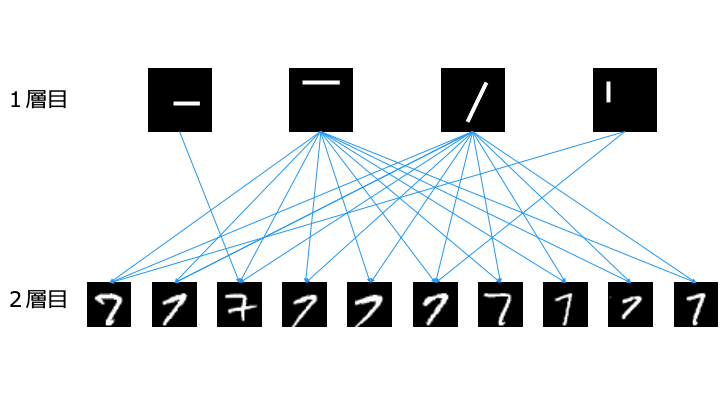
そのため、以下のように抽出した特徴を他のパターン認識に流用可能です。
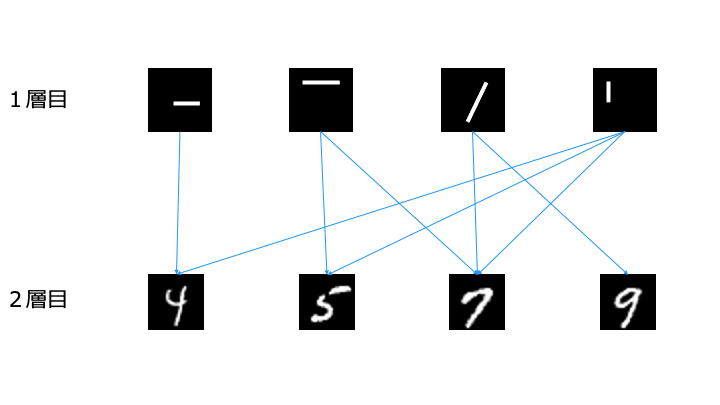
1層目で抽出した特徴は、「7」以外でも流用可能なことがわかります。
関連記事
他のディープラーニング入門記事は以下のとおりです。
- 【ディープラーニング入門1】AI・機械学習・ディープラーニングとは
- 【ディープラーニング入門2】パーセプトロン・ニューラルネットワーク
- 【ディープラーニング入門3】バックプロパゲーション (誤差逆伝播法)
- 【ディープラーニング入門4】学習・重み・ハイパーパラメータの最適化
- 【ディープラーニング入門5】畳み込みニューラルネットワーク (CNN) ←イマココ
参考資料